远近互联网站建设原创文章代写
文章目录
- 算法评估
- DID原理
- 简单实例
- Python实现
算法评估
作为一名算法出身的人,曾长期热衷于算法本身的设计和优化。至于算法的效果评估,通常使用公开数据集做测试,然后对比当前已公开的结果,便可得到结论。
但是在实际落地过程中,却遇到了问题:没有公开数据集;即便有,也依然有必要在实际场景下再做验证,毕竟公开数据集和实际场景往往都有很大区别。
理论上来说,新研发了一个算法后,需要和业务已经在使用的人工经验(被理解为一种特殊的策略)做对比;算法迭代后,前后两个版本的算法也需要做对比。
不失一般性,假设在某个区域内,评价指标为最大化JJJ,此前使用算法A,当前有了新算法B,该如何评估B相比A是否能更好地促进JJJ的提升呢?
理想情况下,是在该区域的两个平行时空中,一个使用算法A,另一个使用算法B,分别得到指标JAJ_AJA和JBJ_BJB。然后比较两个指标的优劣,如果JBJ_BJB指标更好,那么算法B可以被认为是更有利于指标JJJ的提升。
但在任意给定的时间点,该区域实际上只能处于一种状态,即只使用算法A或者只使用算法B,因此只能观察到JAJ_AJA或JBJ_BJB。
因此,需要寻找两个相同的区域,然后分别使用A算法和B算法,再基于得到的指标进行算法优劣的评估。当然,要找到两个相同的区域,在现实中是很困难的;但是如果区域不同,无论控制其多少个参数相同,都有可能让JJJ受到某些未观测参数的影响。
如果退而求其次,不要求完全相同,是否还有机会去科学地评估算法A和B呢?答案是有的,就是本文即将介绍的双重差分法(difference-in-differences,DID)。
DID原理
DID的原理如下图所示。选定两个区域1和2,以算法B的干预时刻为基准,将时间定义为干预前和干预后。在干预后,区域1保持不变,继续使用算法A,最终可以得到A增量;区域2使用算法B后,得到的B增量可以被拆解为两个部分:区域2的自然增量A’,以及算法B带来的纯增量B‘。A’可以理解为不使用算法B时区域2的增量。如果在干预前,两个区域针对指标JJJ的变化趋势保持一致,那么我们可以基于A和此前的变化趋势估计出A’,即做出反事实推断。由于区域2实际的增量B是已知的,因此算法B带来的纯增量为
B′=B−A′B'=B-A'B′=B−A′
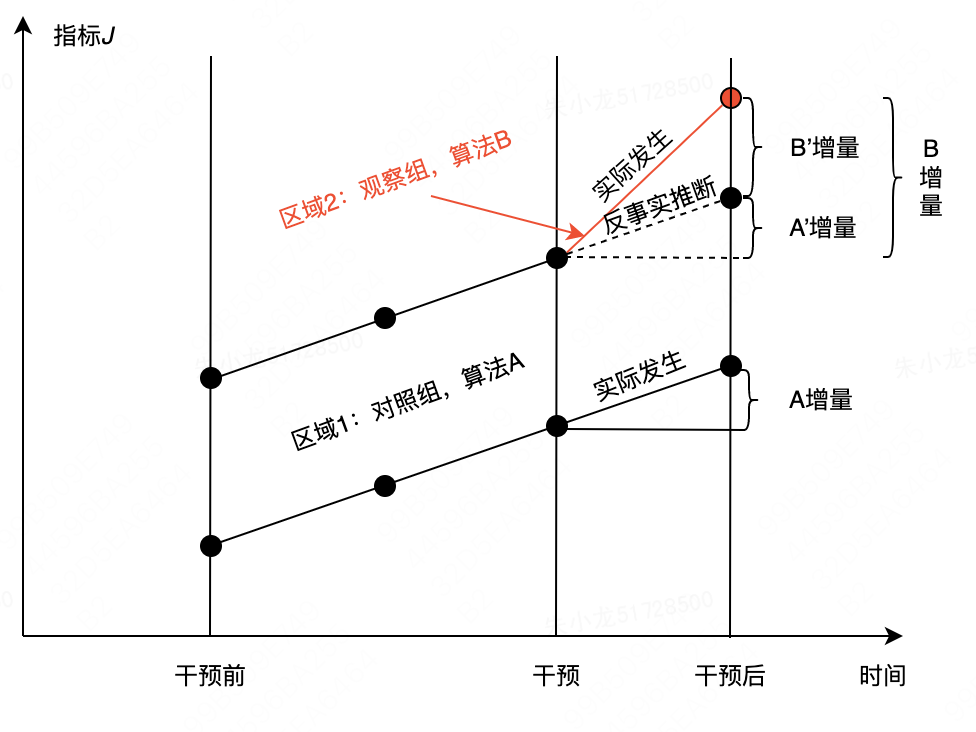
此时,我们发现,不再刻意要求区域1和区域2完全相同,只要求两者的历史指标变化区域保持一致即可,这显著降低了区域选取的难度。
如果使用数学表达式,可以描述为:
Yit=α+δDi+λTt+β(Di×Tt)+ϵitY_{it}=\alpha+\delta D_i+\lambda T_t+\beta(D_i \times T_t)+\epsilon_{it}Yit=α+δDi+λTt+β(Di×Tt)+ϵit
其中,YitY_{it}Yit为JJJ变量;α\alphaα为截距;δ\deltaδ、λ\lambdaλ和β\betaβ为系数值; DiD_iDi为算法B,干预前为0,干预后为1;TtT_tTt为时间,干预前为0,干预后为1;Di×TtD_i \times T_tDi×Tt为交叉项;ϵit\epsilon_{it}ϵit为随机项。
对上式取条件期望后,算法增量(上图中的B’)为β\betaβ,计算过程如下表所示。
| E(Y∣D,T)E(Y|D,T)E(Y∣D,T) | T=0T=0T=0 | T=1T=1T=1 | Δ\DeltaΔ |
|---|---|---|---|
| D=0D=0D=0 | α\alphaα | α+λ\alpha+\lambdaα+λ | λ\lambdaλ |
| D=1D=1D=1 | α+δ\alpha+\deltaα+δ | α+δ+λ+β\alpha+\delta+\lambda+\betaα+δ+λ+β | λ+β\lambda+\betaλ+β |
| Δ\DeltaΔ | δ\deltaδ | δ+β\delta+\betaδ+β | β\betaβ |
显然,如果β>0\beta>0β>0,则认为算法B对指标JJJ有正向促进作用;反之,则认为有负向抵制作用。
简单实例
那么,如何求解β\betaβ值呢?
目前大部分DID的代码都是基于stata实现的。因此,本节主要参考半块土豆切丝的视频,给出一个简单实例的计算过程。
实例描述为:A和B为历史指标的变化保持一致的两个地区,在1994年,B区实行了一项新政策,目标是评估新政策对指标yyy的影响。相关数据如下。
| country | year | y |
|---|---|---|
| A | 1990 | 1342787840 |
| A | 1991 | -1899660544 |
| A | 1992 | -11234363 |
| A | 1993 | 2645775360 |
| A | 1994 | 3008334848 |
| A | 1995 | 3229574144 |
| A | 1996 | 2756754176 |
| A | 1997 | 2771810560 |
| A | 1998 | 3397338880 |
| A | 1999 | 39770336 |
| B | 1990 | 1342787840 |
| B | 1991 | -1518985728 |
| B | 1992 | 1912769920 |
| B | 1993 | 1345690240 |
| B | 1994 | 2793515008 |
| B | 1995 | 1323696384 |
| B | 1996 | 254524176 |
| B | 1997 | 3297033216 |
| B | 1998 | 3011820800 |
| B | 1999 | 3296283392 |
此处先直接给出stata代码如下:
// stata代码gen period = (year>=1994) & !missing(year) // 生成时间虚拟变量D,1994年前为0,反之为1
gen treat = (country>1) & !missing(country) // 生成区域的虚拟变量T,干预为1,反之为0
gen did = period * treat // 生成交叉项D·Tdiff y, t(treat) p(period) // DID回归:diff方式
为了更好地理解上述代码,把基本公式再抄写一遍
Yit=α+δDi+λTt+β(Di×Tt)+ϵitY_{it}=\alpha+\delta D_i+\lambda T_t+\beta(D_i \times T_t)+\epsilon_{it}Yit=α+δDi+λTt+β(Di×Tt)+ϵit
对应到该实例:DDD是政策变量treat,B地区为1,A地区为0,上述第2行代码实现;TTT是时间变量period,1994-1999年为1,1990-1993年为0,第1行代码实现;Di×TtD_i \times T_tDi×Tt是交叉项did,第3行代码实现;β\betaβ的计算由第4行代码实现。
先看一下计算结果。
Number of observations in the DIFF-IN-DIFF: 20Before After Control: 4 6 10Treated: 4 6 108 12
--------------------------------------------------------Outcome var. | y | S. Err. | |t| | P>|t|
----------------+---------+---------+---------+---------
Before | | | | Control | 5.2e+08| | | Treated | 7.7e+08| | | Diff (T-C) | 2.5e+08| 1.0e+09| 0.24 | 0.811
After | | | | Control | 2.5e+09| | | Treated | 2.3e+09| | | Diff (T-C) | -2.0e+08| 8.4e+08| 0.24 | 0.812| | | |
Diff-in-Diff | -4.6e+08| 1.3e+09| 0.34 | 0.737
--------------------------------------------------------
R-square: 0.31
* Means and Standard Errors are estimated by linear regression
**Inference: *** p<0.01; ** p<0.05; * p<0.1输出内容看起来挺复杂,我们主要关注DIFF-in-Diff行、y列和P>|t|列的数值,分别是-4.6e8和0.737。其中-4.6e8即为我们要计算的β\betaβ值;0.737表征的是所得到β\betaβ值的靠谱程度,一般命名为ppp。该值如果小于0.05,表明β\betaβ值是有参考价值的;反之,无论β\betaβ值为多少,均认为无显著变化。所有情况罗列一遍:
| p>0.05p>0.05p>0.05 | p<0.05p<0.05p<0.05 | |
|---|---|---|
| β>0\beta>0β>0 | 无显著效果 | 显著正向效果 |
| β<0\beta<0β<0 | 无显著效果 | 显著负向效果 |
所以,在该实例中,可以得到结论:该新政策对指标y并没有显著效果。
Python实现
事实上,有了多组period、treat、did和y值之后,要计算β\betaβ,本质就是一个最小二乘法的优化问题。只不过此处,还需要求解ppp值。庆幸的是,该功能并不需要自己编写代码去实现,可以调用statsmodels工具包来求解。
以下为Python计算β\betaβ值的代码:
import statsmodels.formula.api as smf
import pandas as pdif __name__ == '__main__':df = pd.read_excel('test_data_101_1.xlsx')// 生成时间虚拟变量D,1994年前为0,反之为1df['period'] = df['year'].apply(lambda x: 1 if x >= 1994 else 0)// 生成区域的虚拟变量T,干预为1,反之为0df['treat'] = df['country'].apply(lambda x: 1 if x == 'B' else 0)// 生成交叉项D·Tdf['did'] = df['period'] * df['treat']// 调用smf计算beta值df = df[['period', 'treat', 'did', 'y']]model = smf.ols(formula='y ~ period + treat + did', data=df).fit()print(model.summary())
运行以上代码,可以得到
OLS Regression Results
==============================================================================
Dep. Variable: y R-squared: 0.313
Model: OLS Adj. R-squared: 0.184
Method: Least Squares F-statistic: 2.430
Date: Sun, 05 Mar 2023 Prob (F-statistic): 0.103
Time: 22:27:31 Log-Likelihood: -448.21
No. Observations: 20 AIC: 904.4
Df Residuals: 16 BIC: 908.4
Df Model: 3
Covariance Type: nonrobust
==============================================================================coef std err t P>|t| [0.025 0.975]
------------------------------------------------------------------------------
Intercept 5.194e+08 7.31e+08 0.711 0.488 -1.03e+09 2.07e+09
period 2.015e+09 9.44e+08 2.135 0.049 1.42e+07 4.01e+09
treat 2.511e+08 1.03e+09 0.243 0.811 -1.94e+09 2.44e+09
did -4.556e+08 1.33e+09 -0.341 0.737 -3.28e+09 2.37e+09
==============================================================================
Omnibus: 2.990 Durbin-Watson: 2.288
Prob(Omnibus): 0.224 Jarque-Bera (JB): 2.423
Skew: -0.814 Prob(JB): 0.298
Kurtosis: 2.494 Cond. No. 7.66
==============================================================================
主要看did行、coef列和P>|t|列的数值。显然,该结果和stata的计算结果是完全一致的。
