当前位置：首页 > news >正文

哪家专门做特卖的网站?项目推广方式有哪些

news 2025/7/4 16:43:18

哪家专门做特卖的网站?,项目推广方式有哪些,解决网,无毒手机网站1.排序的概念及其运用 1.1排序的概念排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录…

1.排序的概念及其运用

1.1排序的概念

排序：所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。
稳定性：假定在待排序的记录序列中，存在多个具有相同的关键字的记录，若经过排序，这些记录的相对次序保持不变，即在原序列中，r[i]=r[j]，且r[i]在r[j]之前，而在排序后的序列中，r[i]仍在r[j]之前，则称这种排序算法是稳定的；否则称为不稳定的。
内部排序：数据元素全部放在内存中的排序。
外部排序：数据元素太多不能同时放在内存中，根据排序过程的要求不能在内外存之间移动数据的排序。

1.2 常见的排序算法

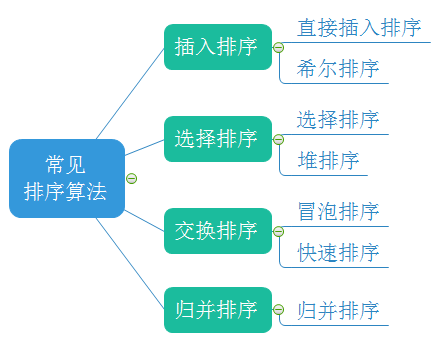
2.常见排序算法的实现

2.1插入排序

1.直接插入排序

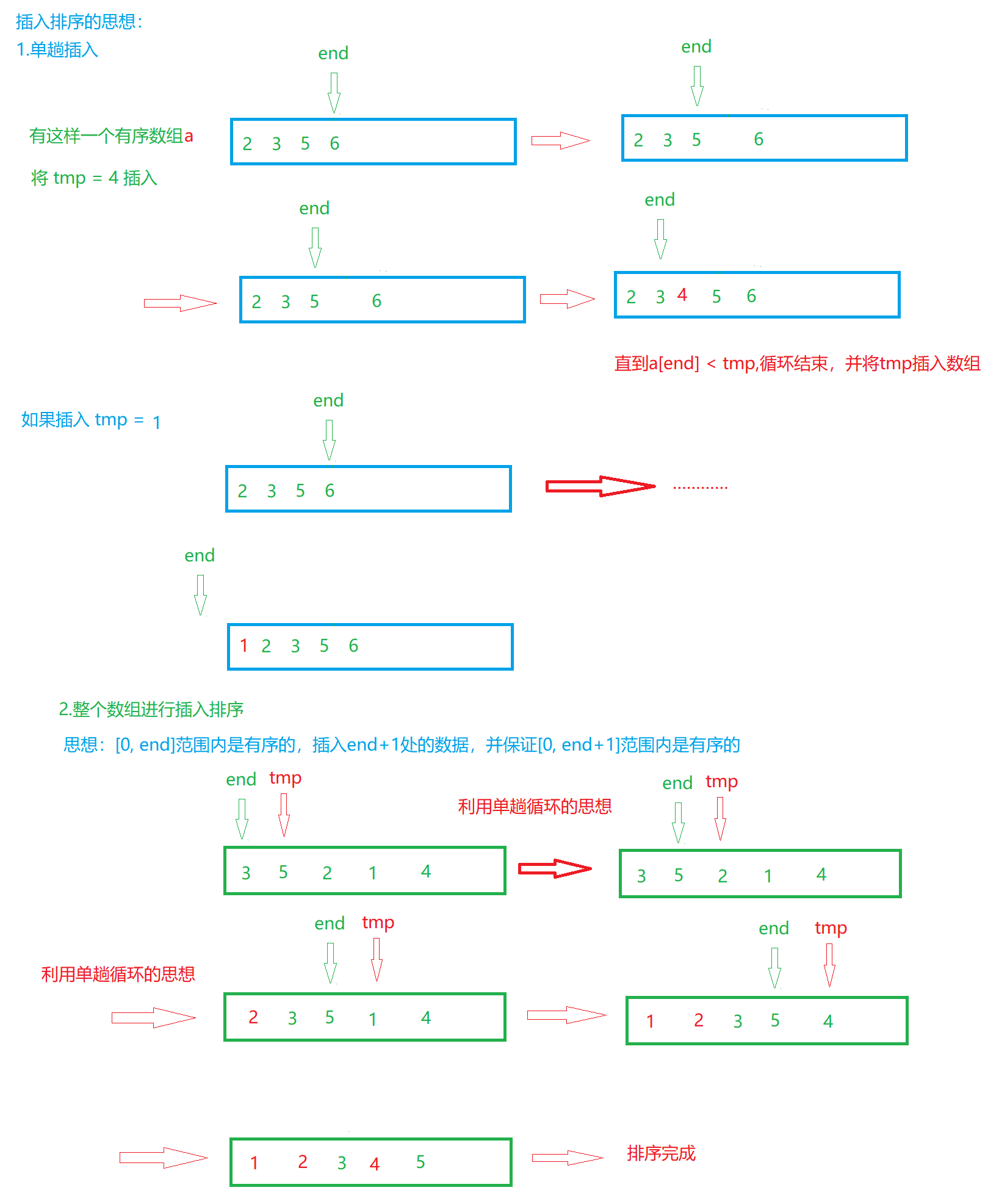
// 最坏时间复杂度O(N^2) -- 原数组是逆序
// 最好时间复杂度O(N) -- 原数组是顺序有序// 直接插入排序
void InsertSort(int* a, int n)
{// 在[0,end]范围内 插入第 end+1 个数据  并使[0, end+1]范围内的数据有序for (int i = 0; i < n - 1; ++i){// 根据上面的图解来理解a[end] 和 tmp的下标int end = i;int tmp = a[end + 1];// 当end >= 0，那么就继续比较a[end]与tmpwhile (end >= 0){// 将数组排列为一个升序数组if (a[end] > tmp){// 如果前一个数据a[end]，大于后一个数据tmp// 直接用end位置的数据覆盖end + 1的数据，保持tmp不发生改变a[end + 1] = a[end];// 迭代--end;}else{break;}}// 当循环结束，end + 1处的数据是旧数据，需要使用tmp更新a[end + 1] = tmp;}
}

打印数组（便于我们来观察排序）

void PrintArray(int* a, int n)
{for (int i = 0; i < n; ++i){printf("%d ", a[i]);}printf("\n");
}

2.希尔排序( 缩小增量排序 )

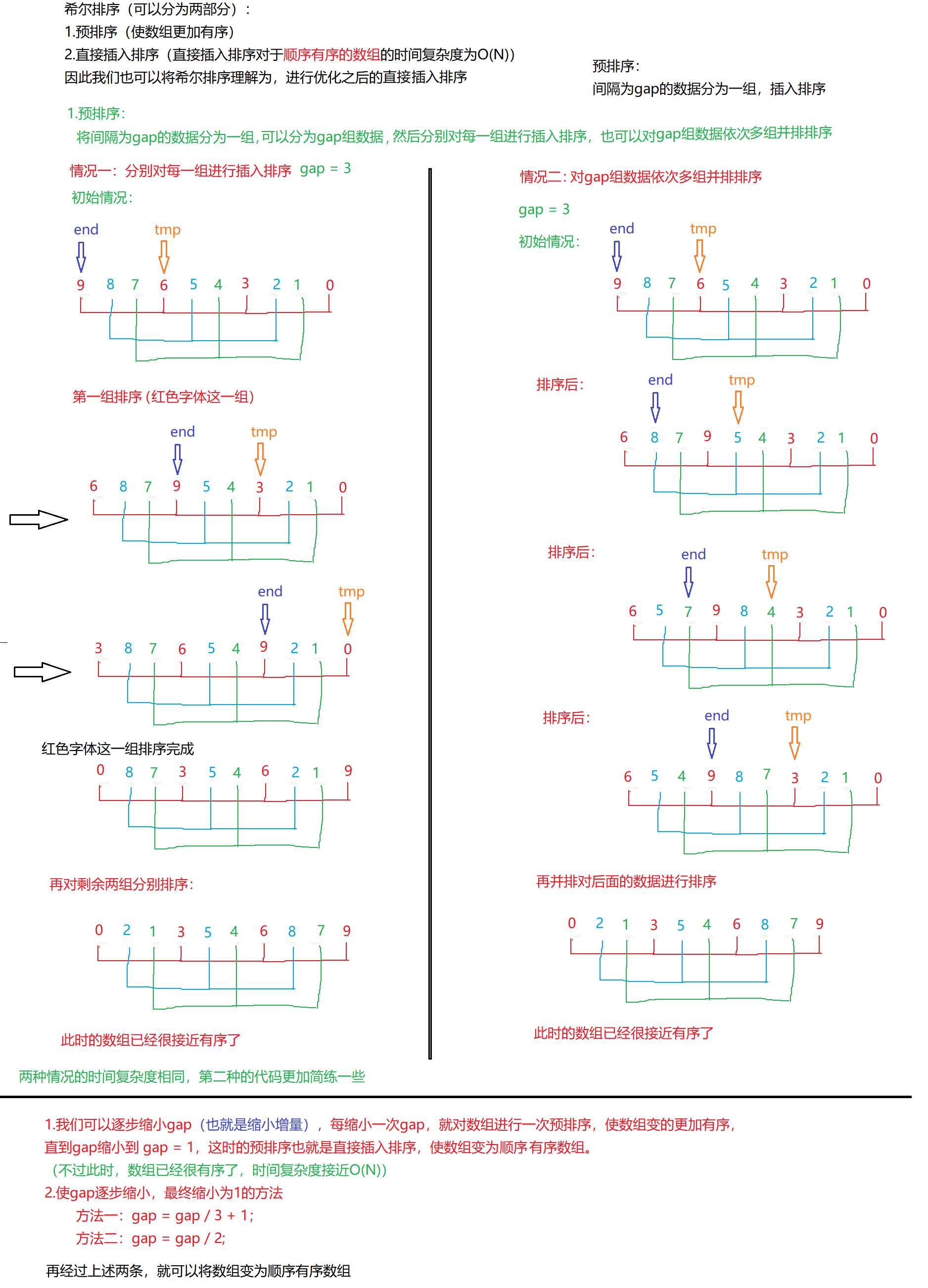
// 情况二：
// 注：希尔排序的时间复杂度，太过复杂，我们可以默认理解希尔排序的时间复杂度为O(N^1.3)，
// 当数据量很大时，是比堆排序O(N*logN)略差的
// 希尔排序的时间复杂度为O(N^1.3)// 这个函数采用的是多组并排排序的方法来实现希尔排序
void ShellSort(int* a, int n)
{// 将间隔为gap的数据分为一组int gap = n;// gap > 1  预排序// gap == 1 直接插入排序// 当while循环结束，说明缩小gap间隙最终为1，数组已经很接近有序了while (gap > 1){// 下面是缩小间隙的两种方法，本文采用第二种// gap = gap / 2;gap = gap / 3 + 1;       // 当for循环结束，gap为n的所有组数据就排列好了// 下面for循环的算法就是，直接插入排序的算法，// 只是改变了a[end]和tmp下标之间的距离for (int i = 0; i < n - gap; ++i){int end = i;int tmp = a[end + gap];// 直到end < 0才可以停止比较while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}
}

// 情况一： 分组进行排序
// 时间复杂度为：O(N^1.3)
void ShellSort(int* a, int n)
{int gap = n;while (gap > 1){//gap = gap / 2;gap = gap / 3 + 1;// 间隔为gap的数据// 当j改变，就是代表一组数据排列完成，将要对下一组数据进行排序for (int j = 0; j < gap; ++j){// 间隔为gap一组排序for (int i = j; i < n - gap; i += gap){int end = i;int tmp = a[end + gap];while (end >= 0){if (a[end] > tmp){a[end + gap] = a[end];end -= gap;}else{break;}}a[end + gap] = tmp;}}}
}

2.2 选择排序

1.直接选择排序

基本思想：

每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

直接选择排序:

在元素集合array[i]–array[n-1]中选择关键码最大(小)的数据元素
若它不是这组元素中的最后一个(第一个)元素，则将它与这组元素中的最后一个（第一个）元素交换
在剩余的array[i]–array[n-2]（array[i+1]–array[n-1]）集合中，重复上述步骤，直到集合剩余1个元素

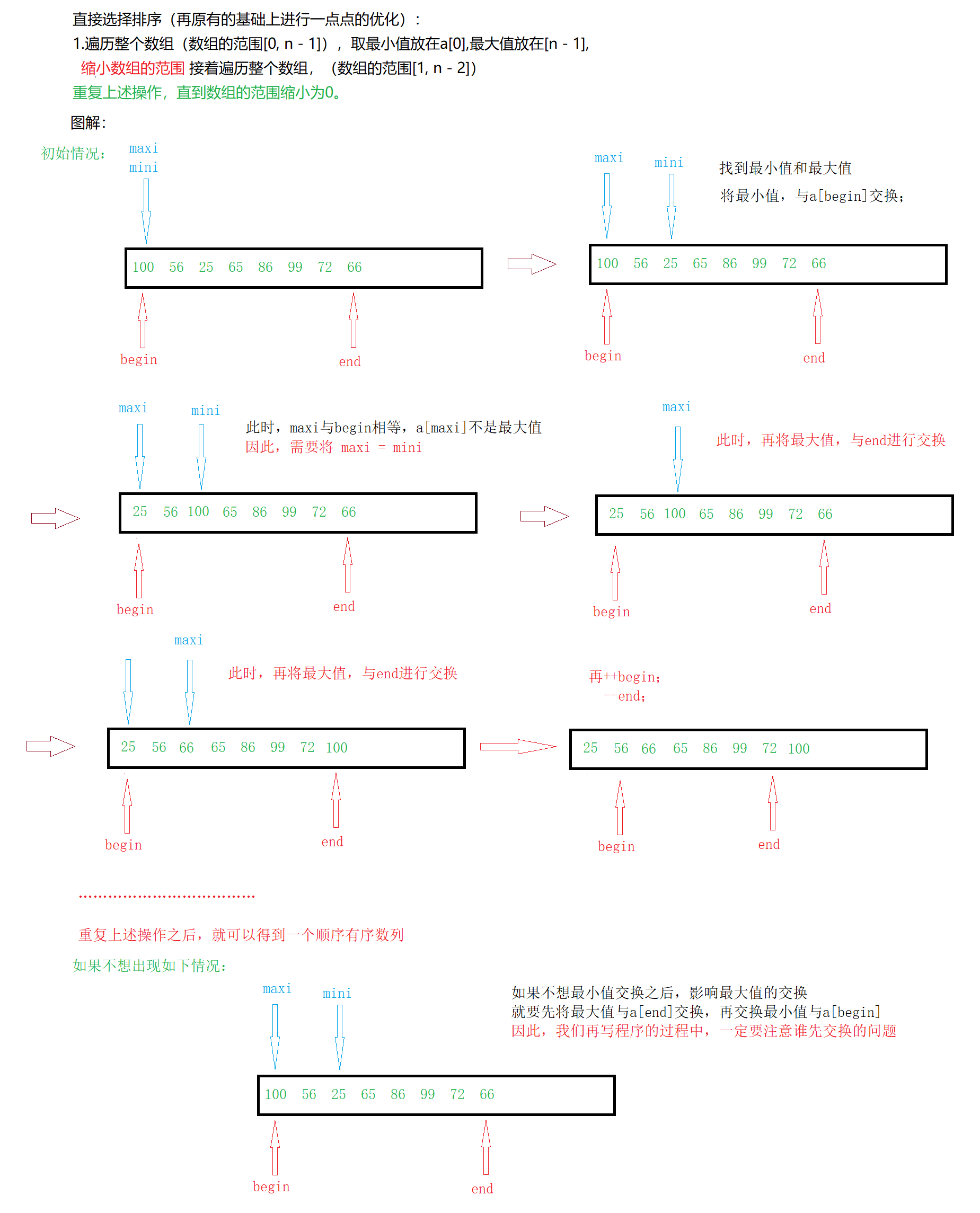
// 直接选择排序最坏时间复杂度：O(N^2)
// 直接选择排序最好时间复杂度：O(N^2)
void SelectSort(int* a, int n)
{// 初始化begin和end下标int begin = 0, end = n - 1;// 只有begin小于end时，才可以继续while (begin < end){// 选出最小的放begin位置// 选出最大的放end位置// 将标识最大值和最小值的下标都初始化为beginint mini = begin, maxi = begin;// 当for循环结束时，a[mini]为最小值，a[maxi]为最大值，在[begin,end]范围内for (int i = begin + 1; i <= end; ++i){// 如果为真，那么i下标所在的元素就是最大值，所以更改最大值的下标maxi为iif (a[i] > a[maxi]){maxi = i;}if (a[i] < a[mini]){mini = i;}}// 1.现将最小值a[mini]与初始位置的值进行交换Swap(&a[begin], &a[mini]);// 修正一下maxi// 如果初始位置的值是最大值，由于上面进行了交换,所以此时最大值的下标为mini// 因此，将mini赋值给maxiif (maxi == begin)maxi = mini;// 2.将最大值a[maxi]与末尾位置的值进行交换Swap(&a[end], &a[maxi]);// 迭代++begin;--end;}
}

2.堆排序

void AdjustDown(int* a, int n, int parent)
{int minChild = parent * 2 + 1;while (minChild < n){// 找出小的那个孩子if (minChild + 1 < n && a[minChild + 1] > a[minChild]){minChild++;}if (a[minChild] > a[parent]){Swap(&a[minChild], &a[parent]);parent = minChild;minChild = parent * 2 + 1;}else{break;}}
}// O(N*logN)
void HeapSort(int* a, int n)
{// 大思路：选择排序，依次选数，从后往前排// 升序 -- 大堆// 降序 -- 小堆// 建堆 -- 向下调整建堆 - O(N)for (int i = (n - 1 - 1) / 2; i >= 0; --i){AdjustDown(a, n, i);}// 选数 N*logNint i = 1;while (i < n){Swap(&a[0], &a[n - i]);AdjustDown(a, n - i, 0);++i;}
}

关于堆排序请查看作者的另一篇文章，堆排序。

2.3 交换排序

1.冒泡排序

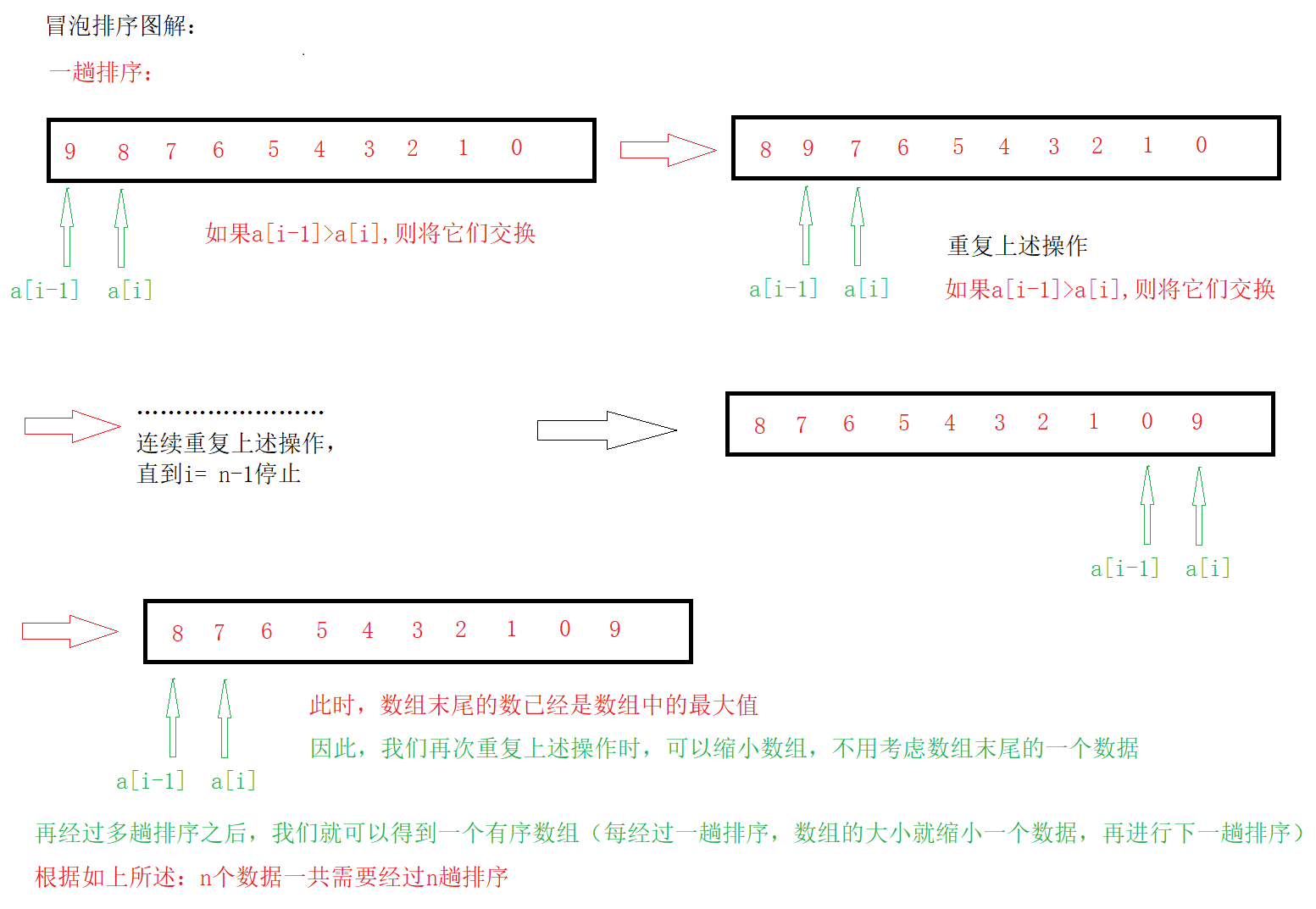
// 交换排序（冒泡排序）
// 冒泡排序最坏情况的时间复杂度：O(N^2)
// 冒泡最好情况的时间复杂度：O(N)
void BubbleSort(int* a, int n)
{// n是数组中元素的个数// 这个for代表趟数for (int j = 0; j < n; ++j){// 每一趟都会将exchange初始化为0// 如果还有a[i - 1] > a[i]存在，那么exchange就会被修改为1// 但是最后一趟时，数组已经是一个有序的数组了，因此exchange不会被修改int exchange = 0;// for代表了一趟中，a[i]与a[i - 1]迭代比较for (int i = 1; i < n - j; ++i){// a[i - 1]是下标较小的元素，a[i]是下标较大的元素// 当这个条件为真，那么交换两个元素的位置if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0){break;}}
}

2.快速排序

快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法，其基本思想为：任取待排序元素序列中的某元素作为基准值，按照该排序码将待排序集合分割成两子序列，左子序列中所有元素均小于基准值，右子序列中所有元素均大于基准值，然后最左右子序列重复该过程，直到所有元素都排列在相应位置上为止。

1.hoare版本

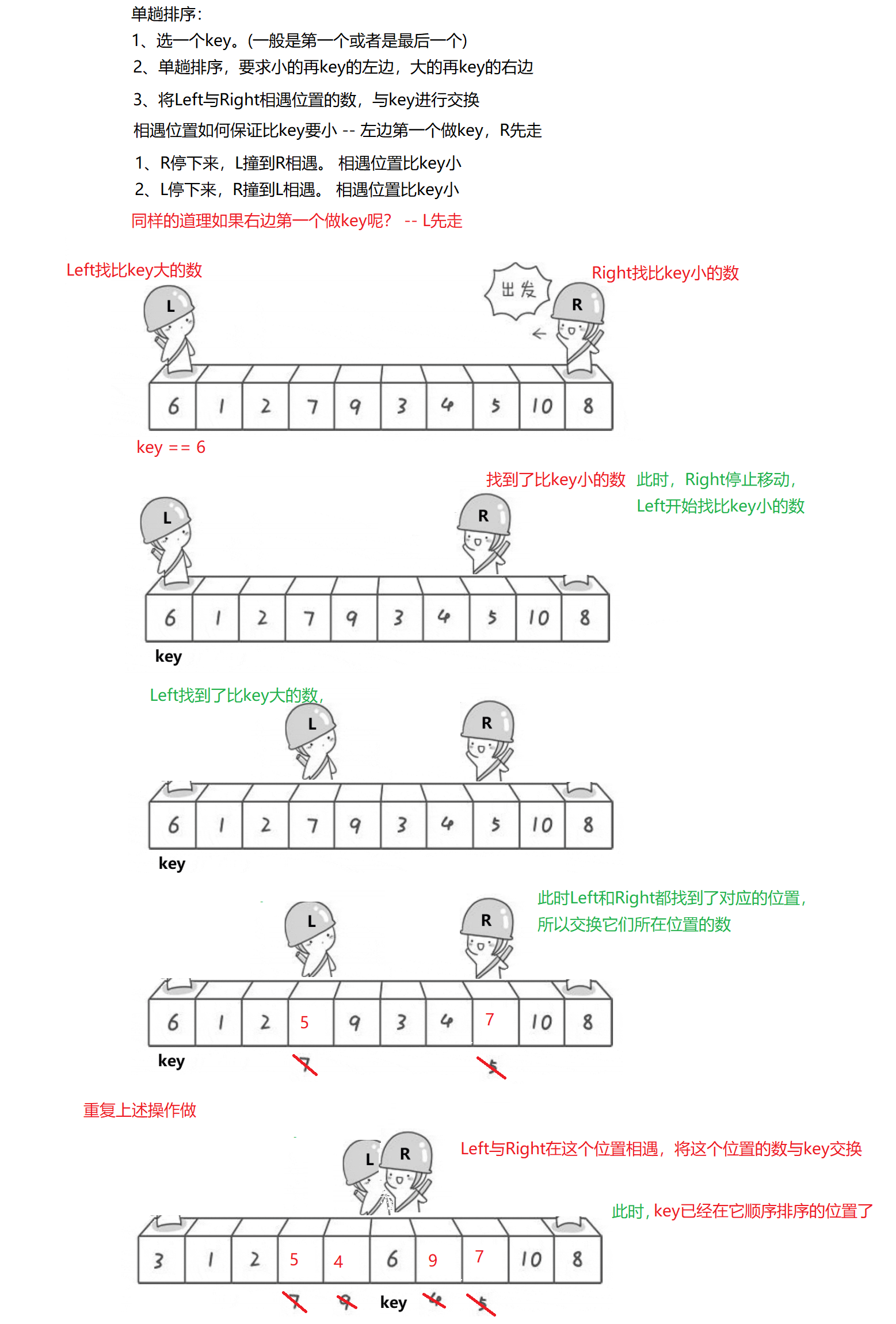
void Swap(int* p1, int* p2)
{int tmp = *p1;*p1 = *p2;*p2 = tmp;
}// PartSort函数，是一趟（想要利用上述的方法将这个数组的元素排序，还需要很多趟，具体看后续的解释）
// 返回left和right相遇节点的下标
int PartSort(int* a, int left, int right)
{// 将左侧的下标定义为keyi下标int keyi = left;// 当left等于right说明两个人相遇了，那么就停止循环while (left < right){// Right需要找比a[keyi]小的数// 因此，如果a[right] >= a[keyi]为真，那么就继续循环// 注意：在循环的过程中一定要保证left < right，否则就没有意义了while (left < right && a[right] >= a[keyi]){--right;}// Lift需要找比a[keyi]大的数while (left < right && a[left] <= a[keyi]){++left;}// 如果此时left < right为真，那么就交换a[left]和a[right]if (left < right)Swap(&a[left], &a[right]);}// 此时，left和right都是相遇节点的下标，// 使用left赋值给meetiint meeti = left;// 将相遇节点的数据与keyi下标的数据进行交换Swap(&a[meeti], &a[keyi]);return meeti;
}

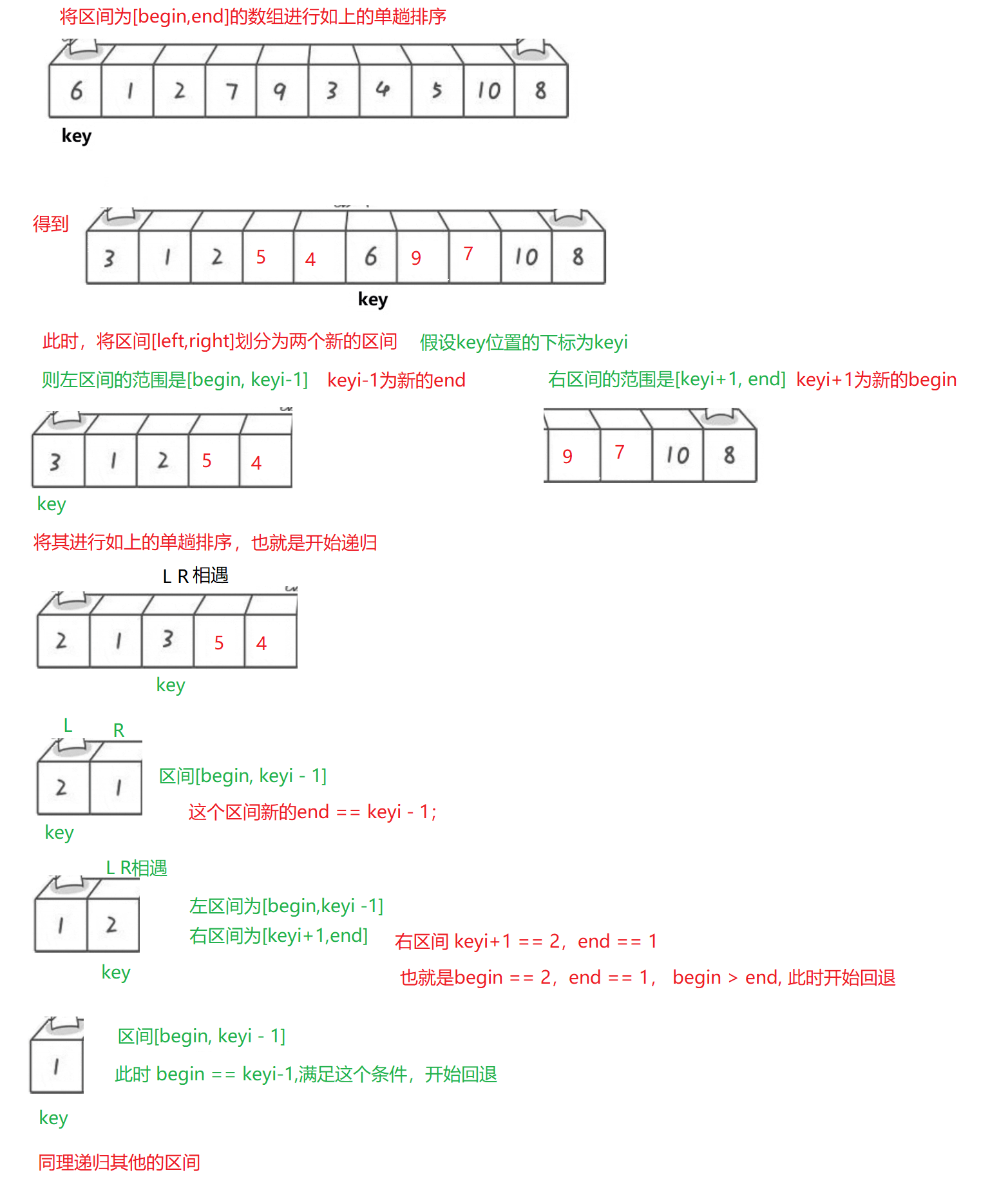
// 快速排序
void QuickSort(int* a, int begin, int end)
{// 必须满足begin小于end// 否则，就返回if (begin >= end){return;}// 先使用PartSort()函数对[begin,end]区间的数进行一趟排序// PartSort()的返回值是meeti，也就是相遇节点的下标，将其存放到keyiint keyi = PartSort(a, begin, end);// 以keyi为分割点，将[begin,end]区间分割为下面两个区间// [begin, keyi-1] keyi [keyi+1, end]// 左区间递归，和右区间递归QuickSort(a, begin, keyi - 1);QuickSort(a, keyi+1, end);
}

快速排序的优化

// 优化之后的代码// 三数取中
int GetMidIndex(int* a, int left, int right) 
{// 数组中间的数的下标就是midint mid = left + (right - left) / 2;if (a[left] < a[mid]){// 此时a[mid]已经大于a[left]，那么只要满足a[mid] < a[right]，就返回a[mid]的下标// 满足a[left] > a[right],也就是a[mid]>a[left] > a[right],就返回a[left]的下标// 都不满足，也就是a[right]<a[left]<a[mid],就返回a[right]的下标if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]){return left;}else{return right;}}else // a[left] >= a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]){return left;}else{return right;}}
}// [left, right] -- O(N)
// hoare
// PartSort1函数，是一趟(单趟排序)
int PartSort1(int* a, int left, int right) 
{// 三数取中，得到left，right，left + (right - left) / 2中，中间大的哪个数int mid = GetMidIndex(a, left, right);// 此处的mid就是指中间大的哪个数的下标//printf("[%d,%d]-%d\n", left, right, mid);// 将中间大的数，放在数组的最左侧Swap(&a[left], &a[mid]);// keyi依旧是最左侧的数的下标（继承优化前的代码，不需要做出改动）int keyi = left;while (left < right){// R找小while (left < right && a[right] >= a[keyi]){--right;}// L找大while (left < right && a[left] <= a[keyi]){++left;}if (left < right)Swap(&a[left], &a[right]);}int meeti = left;Swap(&a[meeti], &a[keyi]);return meeti;
}// 快速排序函数
void QuickSort(int* a, int begin, int end)   // 分区间递归
{// 必须保证begin >= end为假，才可以继续迭代if (begin >= end){return;}// 8的取值，参考经验，8比较合适// 当[begin,end]区间的元素小于等于8时，这个时候再分小区间，后三层小区间有很多个// 为了减小栈的开销，当end - begin <= 8为真时，采用直接插入排序来将数组进行排序（此时的数组已经很接近有序了，因此使用直接插入排序，并不会降低太多的效率）if (end - begin <= 8) {// 小区间优化，最后三层用直接插入排序InsertSort(a + begin, end - begin + 1);}else{// 先使用PartSort()函数对[begin,end]区间的数进行一趟排序// PartSort()的返回值是meeti，也就是相遇节点的下标，将其存放到keyiint keyi = PartSort1(a, begin, end);// 以keyi为分割点，将[begin,end]区间分割为下面两个区间// [begin, keyi-1] keyi [keyi+1, end]// 迭代左区间// 迭代右区间QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);}
}

2.挖坑法（重要）

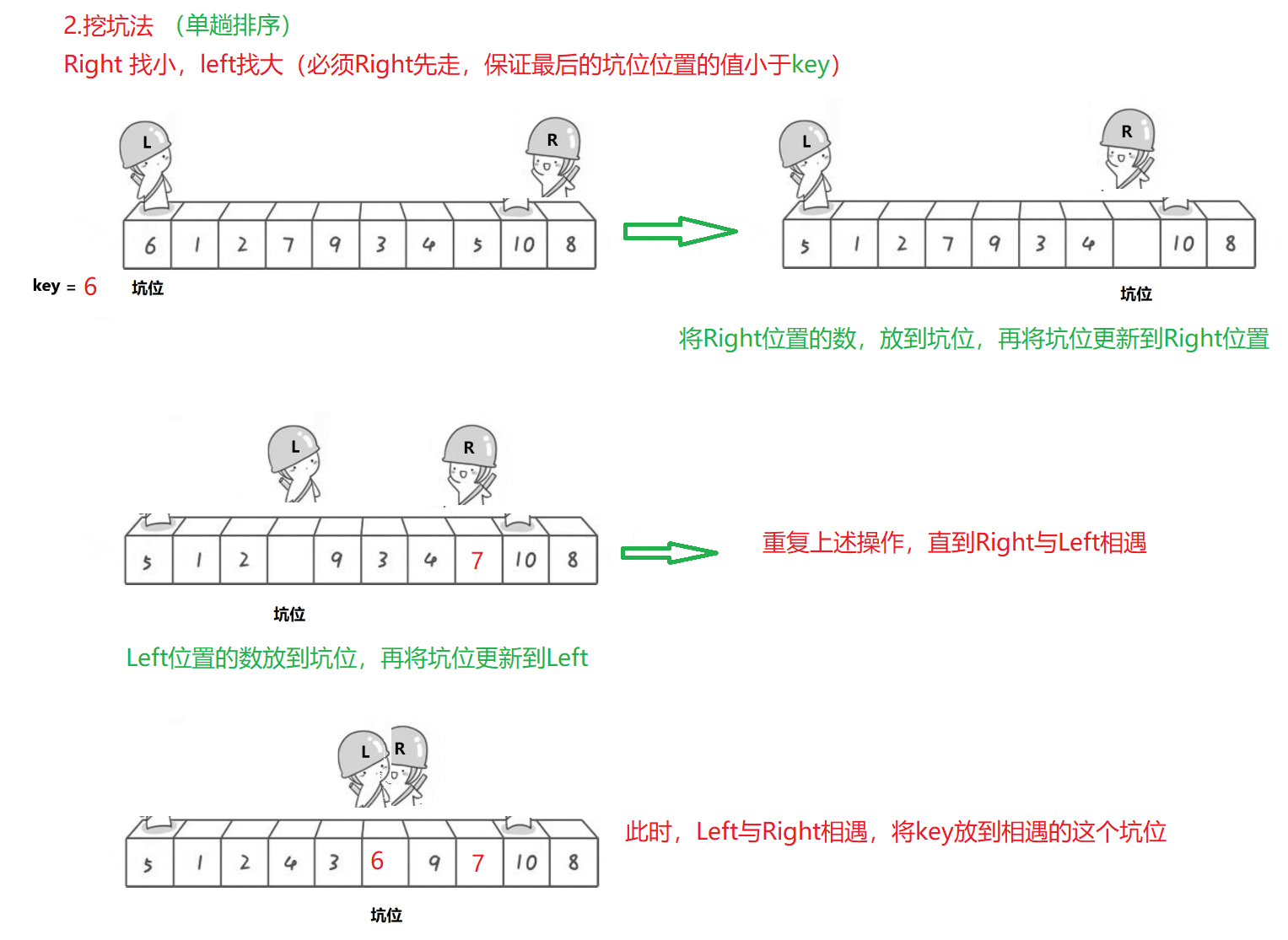
// 三数取中
int GetMidIndex(int* a, int left, int right) 
{int mid = left + (right - left) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]){return left;}else{return right;}}else // a[left] >= a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]){return left;}else{return right;}}
}// 挖坑法
int PartSort2(int* a, int left, int right)
{// 三数取中int mid = GetMidIndex(a, left, right);Swap(&a[left], &a[mid]);// 将key值初始化为a[left]// 将坑位的下标hole初始化为leftint key = a[left];int hole = left;while (left < right){// 右边找小，填到左边坑while (left < right && a[right] >= key){--right;}a[hole] = a[right];// 此时right对应的下标成为新的坑位hole = right;// 左边找大，填到右边坑while (left < right && a[left] <= key){++left;}a[hole] = a[left];hole = left;}// 当left和right相遇，将key值放入这个坑位（最后的这个坑位）a[hole] = key;return hole;
}// [begin, end]
void QuickSort(int* a, int begin, int end)   // 分区间递归
{if (begin >= end){return;}if (end - begin <= 8) // 8的取值，参考经验，8比较合适{InsertSort(a + begin, end - begin + 1);// 小区间优化，最后三层用插入排序}else{int keyi = PartSort2(a, begin, end);//[begin, keyi-1] keyi [keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);}
}

3.前后指针法

本质就是cur指向的值小于key，prev指向的值大于key，那么交换cur和prev所指向的值

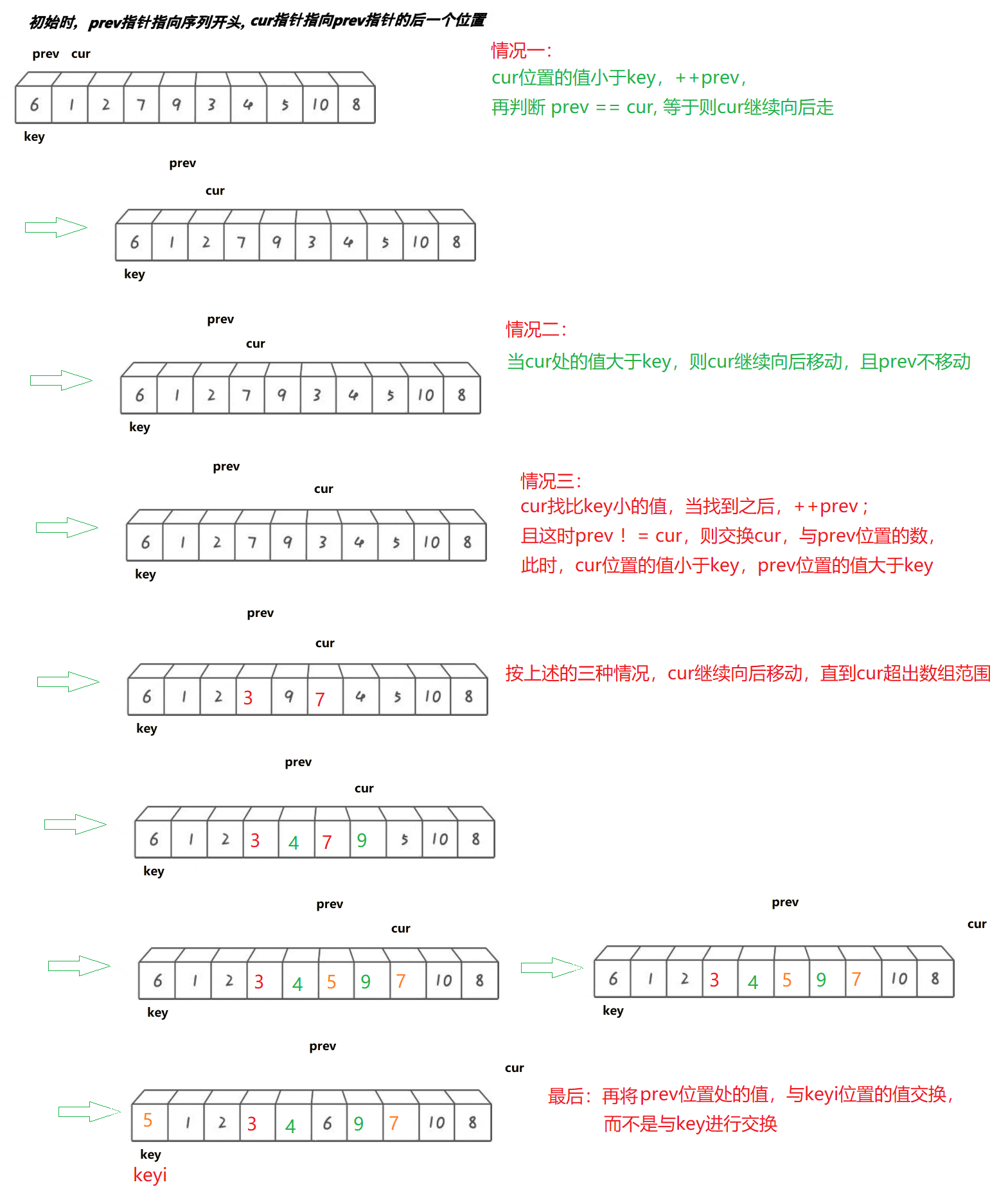
// 三数取中
int GetMidIndex(int* a, int left, int right) 
{int mid = left + (right - left) / 2;if (a[left] < a[mid]){if (a[mid] < a[right]){return mid;}else if (a[left] > a[right]){return left;}else{return right;}}else // a[left] >= a[mid]{if (a[mid] > a[right]){return mid;}else if (a[left] < a[right]){return left;}else{return right;}}
}// 前后指针法
int PartSort3(int* a, int left, int right)
{// 三数取中int mid = GetMidIndex(a, left, right);Swap(&a[left], &a[mid]);int keyi = left;int prev = left;int cur = left + 1;while (cur <= right){// 找小if (a[cur] < a[keyi] && ++prev != cur)Swap(&a[cur], &a[prev]);++cur;}Swap(&a[keyi], &a[prev]);return prev;
}// [begin, end]
void QuickSort(int* a, int begin, int end)   // 分区间递归
{if (begin >= end){return;}if (end - begin <= 8) // 8的取值，参考经验，8比较合适{InsertSort(a + begin, end - begin + 1);// 小区间优化，最后三层用插入排序}else{int keyi = PartSort3(a, begin, end);//[begin, keyi-1] keyi [keyi+1, end]QuickSort(a, begin, keyi - 1);QuickSort(a, keyi + 1, end);}
}

3.快速排序（非递归的方法）

void QuickSortNonR(int* a, int begin, int end)
{// 栈结构对象在堆上面开辟空间，不用担心栈溢出ST st;  // 初始化栈StackInit(&st);// 将区间[begin,end]的左右断点存储到栈对象中StackPush(&st, begin);StackPush(&st, end);// 直到栈为空，循环结束（意味着所有的小区间都已经排序完毕了）while (!StackEmpty(&st)){// 因为压栈的时候是先压入的左端点，再压入右端点（都是下标）// 所以，从栈顶拿出数据时，是先拿出右端点，再拿出左端点（都是下标）int right = StackTop(&st);StackPop(&st);int left = StackTop(&st);StackPop(&st);/*if (left >= right)       // 在取出时，判断区间是否满足排序要求{continue;}*/// 根据拿出的区间断点，对这个区间的数据进行一趟排序int keyi = PartSort3(a, left, right);// 排序完之后，得到下标keyi，根据下标keyi将之前的区间重新分为两个新区间// 再将两个新区间的左右端点入栈，就可以重复上述的操作，完成所有区间的排序// [left, keyi-1] keyi [keyi+1,right]// 在存入时，判断区间是否满足存入要求，避免无效存储，和取出判断if (keyi + 1 < right)     {StackPush(&st, keyi + 1);StackPush(&st, right);}// 在存入时，判断区间是否满足存入要求，避免无效存储，和取出判断if (left < keyi- 1)     {StackPush(&st, left);StackPush(&st, keyi - 1);}}// 最后，销毁栈对象开辟的空间，防止内存泄漏StackDestroy(&st);
}

2.4 归并排序

基本思想：

归并排序（MERGE-SORT）是建立在归并操作上的一种有效的排序算法,该算法是采用分治法（Divide and

Conquer）的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有

序，再使子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。归并排序核心步骤：

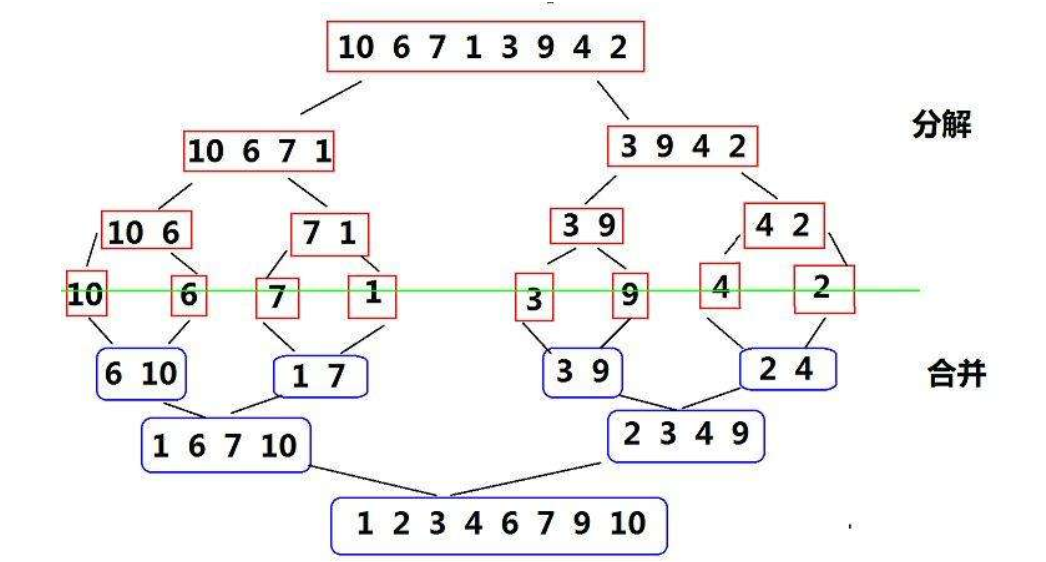
归并排序（递归的方法

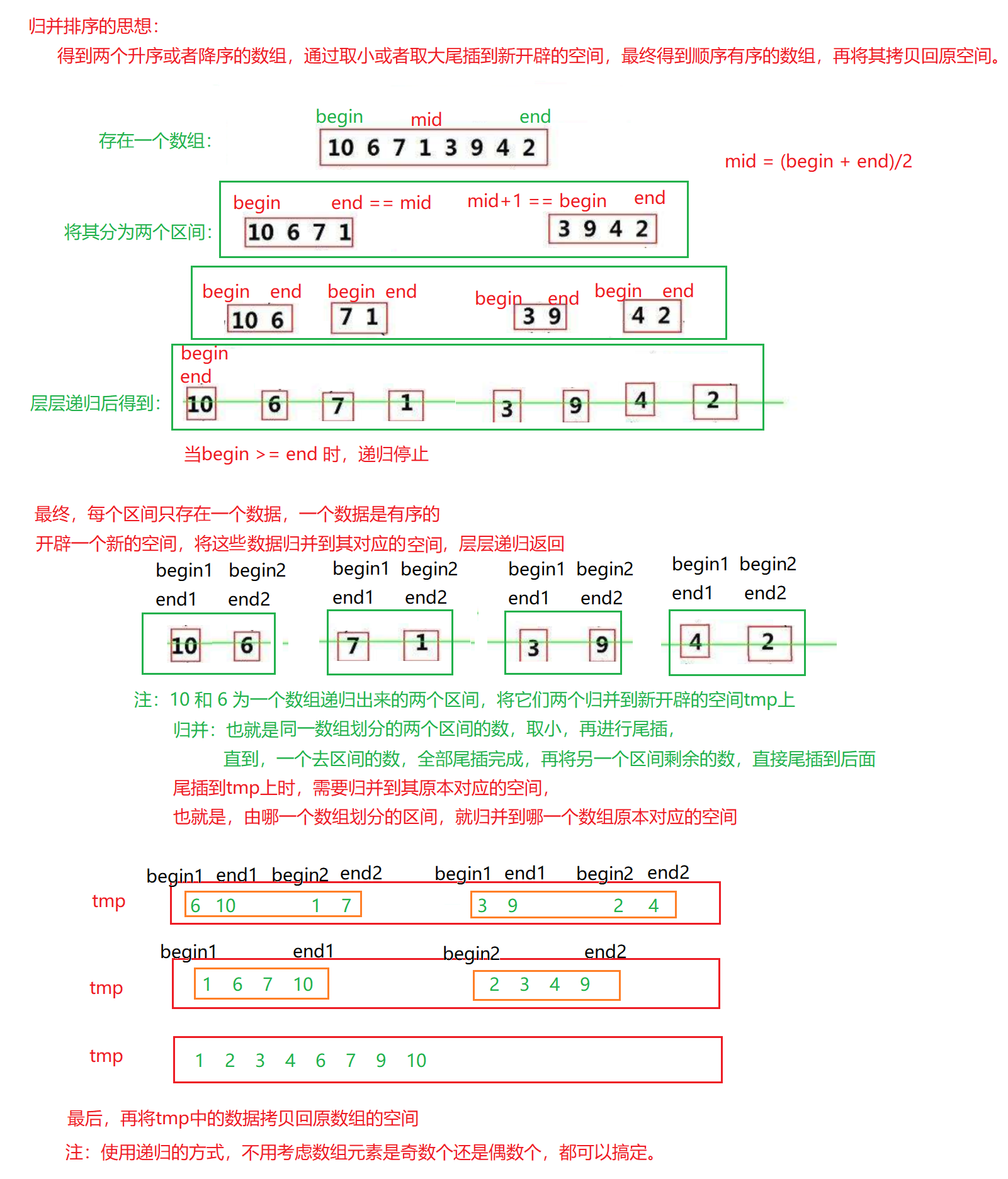
归并排序（递归的方法）

#define _CRT_SECURE_NO_WARNINGS#include<stdio.h>// 归并排序（递归的方法）
// 函数_MergeSort是函数MergeSort的一部分
void _MergeSort(int* a, int begin, int end, int* tmp)
{// 必须保证begin >= end为假，否则就直接返回if (begin >= end)return;// 取数组的中间下标，将数组分为两个区间int mid = (end + begin) / 2;// [begin, mid] [mid+1, end]// 左区间迭代和右区间迭代_MergeSort(a, begin, mid, tmp);_MergeSort(a, mid + 1, end, tmp);// 迭代完之后，此时有无数个被分裂的小区间，每个区间只有一个数// 归并 取两个区间中小的数值尾插到tmp中（tmp是一个临时数组，临时存放这些归并的数据的）// 注：因为左右区间是迭代的，所以begin,mid,end的大小对应相应的迭代，当回到迭代最初的地方// 那么[begin, mid] [mid+1, end]这两个区间的数已经是有序的了// [begin, mid] [mid+1, end]int begin1 = begin, end1 = mid;int begin2 = mid + 1, end2 = end;// 两个区间的数归并时，必须满足 begin1 <= end1 && begin2 <= end2int i = begin;while (begin1 <= end1 && begin2 <= end2){// 取两个区间中较小的数尾插到tmp中if (a[begin1] <= a[begin2]){// 后置++，先使用，后++tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}// 如果区间2的数尾插完了，但是区间1的数没有尾插完，那么这里将区间一剩余的数尾插到tmp中while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}// 拷贝回原数组 -- 归并哪部分就拷贝哪部分回去memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int));
}void MergeSort(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int) * n);if (tmp == NULL){perror("malloc fail");return;}// void _MergeSort(int* a, int begin, int end, int* tmp)_MergeSort(a, 0, n - 1, tmp);free(tmp);tmp = NULL;
}void PrintArray(int* a, int n)
{for (int i = 0; i < n; ++i){printf("%d ", a[i]);}printf("\n");
}void TestMergeSort()
{int a[] = { 100, 56, 25, 86, 99, 72, 66 };int n = sizeof(a) / sizeof(int);MergeSort(a, n);PrintArray(a, n);
}int main()
{TestMergeSort();return 0;
}

memcpy()的用法

在C语言中，memcpy() 函数用于在内存之间复制一定数量的字节。它的原型如下：

void *memcpy(void *dest, const void *src, size_t n);

dest 是目标内存区域的指针，指向要复制到的位置。
src 是源内存区域的指针，指向要复制的数据的起始位置。
n 是要复制的字节数。

memcpy() 函数将源内存区域中的数据复制到目标内存区域中。它返回目标内存区域的起始位置（即 dest 指针），这使得可以将 memcpy() 作为一个表达式的一部分来使用。

以下是一个示例代码，演示了如何使用 memcpy() 函数复制内存中的数据：

#include <stdio.h>
#include <string.h>int main() {char src[] = "Hello, world!";char dest[20];// 将 src 中的数据复制到 dest 中memcpy(dest, src, strlen(src) + 1);// 打印复制后的字符串printf("Copied string: %s\n", dest);return 0;
}

在这个示例中，我们将字符串 "Hello, world!" 从源内存区域 src 复制到目标内存区域 dest 中，然后打印出复制后的字符串。

归并排序（非递归的方式）

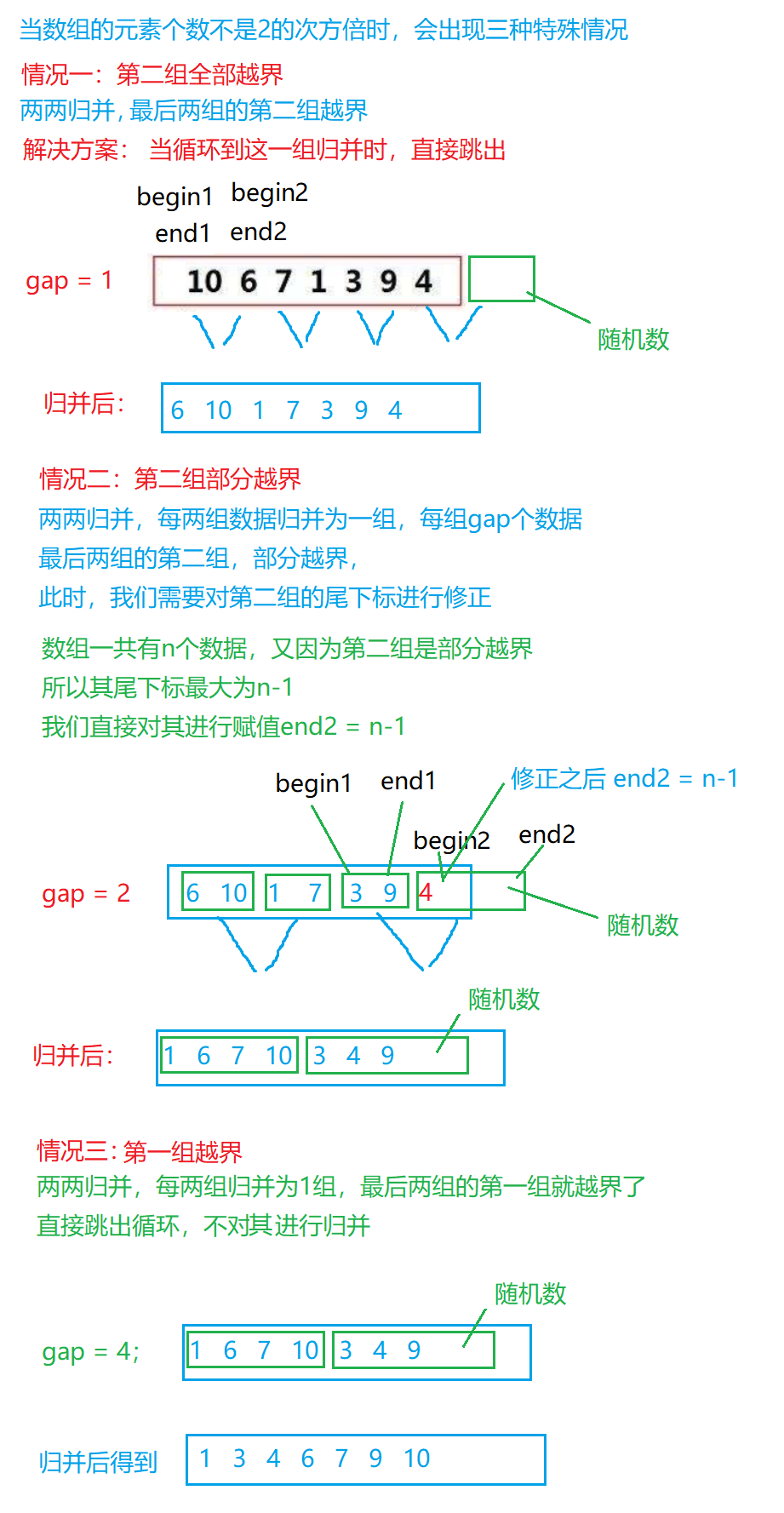
void MergeSortNonR(int* a, int n)
{int* tmp = (int*)malloc(sizeof(int)*n);if (tmp == NULL){perror("malloc fail");return;}int gap = 1;while (gap < n){// 首次循环时，每个区间只有一个数，此时gap=1// 当归并一次之后，每个区间就有两个数，那时就将gap扩大两倍// gap个数据  gap个数据归并// gap每改变一次，进行一次for循环for (int j = 0; j < n; j += 2 * gap){// 归并两个区间 取较小的值尾插到tmp// j为区间一的区间为[j,j + gap - 1]// 区间二的区间为[j + gap,j + 2 * gap - 1]int begin1 = j, end1 = j + gap - 1;int begin2 = j + gap, end2 = j + 2 * gap - 1;// 当归并到最后两组的数据，并且第一组就完全越界了// 那么不需要进行归并，直接跳出循环就可以if (end1 >= n){printf("[%d,%d]", begin1, n-1);break;}// 第二组全部越界，直接跳出循环就可以// 此时的第一组数据必然是有序的if (begin2 >= n){printf("[%d,%d]", begin1, end1);break;}// 第二组部分越界if (end2 >= n){// 修正一下end2，继续归并（第二组最后一个数的下标，最大为n-1）end2 = n - 1;}printf("[%d,%d][%d,%d] ", begin1, end1, begin2, end2);int i = j;while (begin1 <= end1 && begin2 <= end2){if (a[begin1] <= a[begin2]){tmp[i++] = a[begin1++];}else{tmp[i++] = a[begin2++];}}while (begin1 <= end1){tmp[i++] = a[begin1++];}while (begin2 <= end2){tmp[i++] = a[begin2++];}// 拷贝回原数组 -- 归并哪部分就拷贝哪部分回去memcpy(a+j, tmp+j, (end2-j+1)*sizeof(int));}// 扩大区间范围gap *= 2;printf("\n");}free(tmp);tmp = NULL;
}