当前位置：首页 > news >正文

个人简历模板word格式免费下载seo推广怎么做视频教程

news 2025/7/12 22:19:05

个人简历模板word格式免费下载,seo推广怎么做视频教程,ios6软件下载网站,html总结心得体会小短篇Splay 简介 Splay（伸展树），又叫做分裂树，是一种自调整形式的二叉查找树，满足二叉查找树的性质：一个节点左子树的所有节点的权值，均小于这个节点的权值。且其右子树所有节点的权值，均…

Splay 简介

Splay（伸展树），又叫做分裂树，是一种自调整形式的二叉查找树，满足二叉查找树的性质：一个节点左子树的所有节点的权值，均小于这个节点的权值。且其右子树所有节点的权值，均大于这个节点的权值。
因此Splay的中序遍历是一个递增序列。

Splay可以用来维护实链剖分（LCT）等，作为普通平衡树，它的优势在于不需要记录用于平衡树的冗余信息。

Splay维护一个有序集合，支持如下操作：

向集合中添加一个数
删除集合中的一个数
求出一个数的排名
根据排名求出这个数
查找一个数的前驱
查找一个数的后继

Splay原理以及实现

模板题

约定

为了代码简洁以及安全，我们用数组模拟Splay，并且做出规定如下性质：

安全性：不在Splay上的节点，以及被删除的节点，其所有信息应该被清空。
保证：我们保证函数不可能被非法调用，或者所有可能的非法调用是无害的，因此不需要在被调用的函数内部进行特判。
例如：我们保证get(u)中，u一定有父亲。
例如：push_up(0)是无害的。
代码重用：我们尽可能的保证代码重用
节点从1开始编号，0号节点可能有多余的子孙/后代信息，但是其val,cnt,siz信息始终为0。

或许每一个约定都并不是完全必要的。

节点：node

Splay上的一个节点(node)维护这样几个信息：

fa：这个节点的父亲编号，fa=0表示没有父亲
ch[0]：节点的左儿子编号，ch[0]的别名是l，若l=0表示没有左儿子
ch[1]：节点的右儿子编号，ch[1]的别名是r，若r=0表示没有右儿子
val：节点的权值
cnt：节点权值在集合中出现的次数
siz：以此节点为根的子树的大小
成员函数set(v,c,s)：用来初始化节点信息，使得val=v,cnt=c,siz=s，并且让fa=l=r=0。其中c和s的默认值为1

const int N=2e6;
struct node {int fa,ch[2],val,cnt,siz;int&l=ch[0],&r=ch[1];void set(int v,int c=1,int s=1) {fa=l=r=0;val=v;cnt=c;siz=s;}
} t[N+5];
int tot,root;

左右儿子函数（get）

函数原型：

bool get(int);

函数get(u)返回编号为u的节点是其父亲的左儿子（返回0）或者右儿子（返回1），保证传入的参数u一定有父亲。

函数定义：

bool get(int u) {return t[t[u].fa].r==u;
}

上传（push_up）

函数原型：

void push_up(int);

函数push_up(u)将编号为u节点用自己的两个儿子的信息更新自己的siz信息。当有儿子编号为0时不影响，因为我们保证0号节点的siz信息为0。

函数定义：

void push_up(int u) {t[u].siz=t[t[u].l].siz+t[t[u].r].siz+t[u].cnt;
}

事实上push_up(0)也不影响0节点的siz，因为调用push_up(0)仅在pop函数中root=0时，但此时由于早已del了0节点的左右儿子，因此0节点必然没有左右儿子的信息。

加入节点（add）

函数原型：

void add(int,int,bool);

函数add(fa,son,k)将编号为son的节点加入Splay，并且它是父亲fa的k侧儿子。

函数定义：

void add(int fa,int son,bool k) {t[t[son].fa=fa].ch[k]=son;
}

删除节点（del）

函数原型：

void del(int);

函数del(u)将编号为u的节点从Splay中删除，这需要操作它的父亲和左右儿子，并且将它的三个权值（val,cnt,siz）清空。

函数定义：

void del(int u) {t[t[u].l].fa=t[t[u].r].fa=t[t[u].fa].ch[get(u)]=0;t[u].set(0,0,0);
}

旋转（rotate）

Splay的单次操作复杂度并不是严格 $O(\log n)$ 的，但是Splay依靠其伸展操作(splay)使得总复杂度为均摊 $O(n\log n)$ （而不是期望 $O(n\log n)$ ）的。

在伸展树上的一般操作都基于伸展操作：假设想要对一个二叉查找树执行一系列的查找操作，为了使整个查找时间更小，被查频率高的那些条目就应当经常处于靠近树根的位置。于是想到设计一个简单方法，在每次查找之后对树进行重构，把被查找的条目搬移到离树根近一些的地方。伸展树应运而生。伸展树是一种自调整形式的二叉查找树，它会沿着从某个节点到树根之间的路径，通过一系列的旋转把这个节点搬移到树根去。

函数原型

void rotate(int);

当树是完全二叉树时，单次查询复杂度为 $O(\log n)$
当树是一条链时，单次查询复杂度为 $O (n)$
rotate通过改变树的形态，达到使得Splay的均摊复杂度为 $O(\log n)$ 的目的。

函数rotate(u)将编号为u的节点旋转一次。

旋转原理

首先我们需要记录一个变量k：

k=get(u)

这表明了编号为u的节点是其父亲的哪侧儿子，k=0表示左儿子，k=1表示右儿子。

旋转过程需要保存几个节点编号：

u：当前节点
fa：当且节点的父亲
son：节点t[u]的异侧儿子，即son=t[u].ch[k^1]。例如：如果t[u]是t[fa]的左儿子，那么t[son]就是t[u]的右儿子。
ffa：当前节点的父亲的父亲。

画出一个图来示意一下：
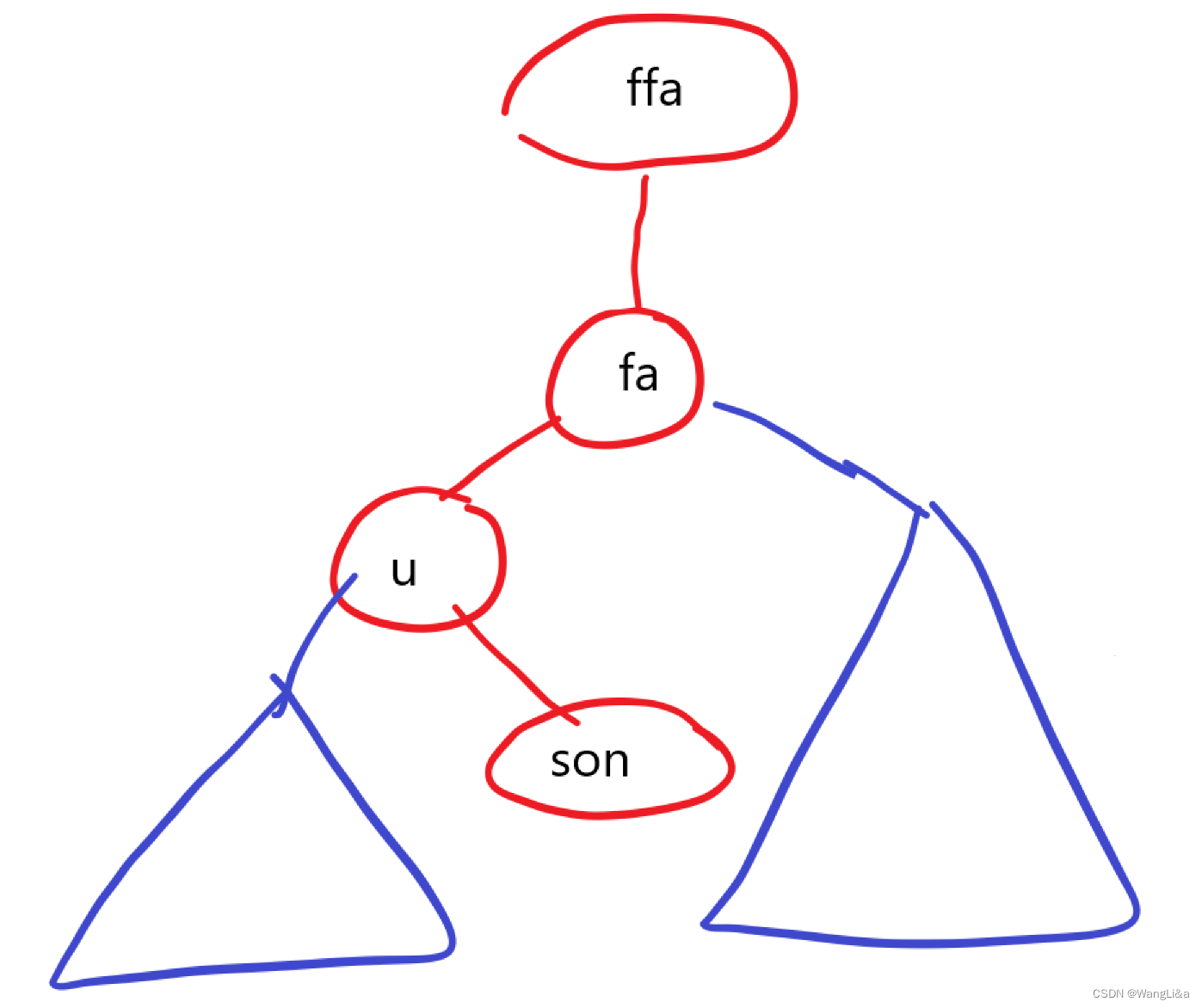
在这里插入图片描述
在这里，t[fa]是t[ffa]的哪侧儿子无关紧要。

接下来我们修改树的形态，完成三步操作：

用u顶替掉原来fa的位置：把u设置为ffa的儿子，fa是哪侧儿子，u就是哪侧儿子。
用fa顶替掉原来son的位置：fa变成u的k^1儿子
把son设为fa的同侧儿子，替代u：son变成fa的k儿子

还是看代码比较好懂：

int k=get(u),son=t[u].ch[k^1],fa=t[u].fa,ffa=t[fa].fa;
add(ffa,u,get(fa));
add(u,fa,k^1);
add(fa,son,k);

画个图：
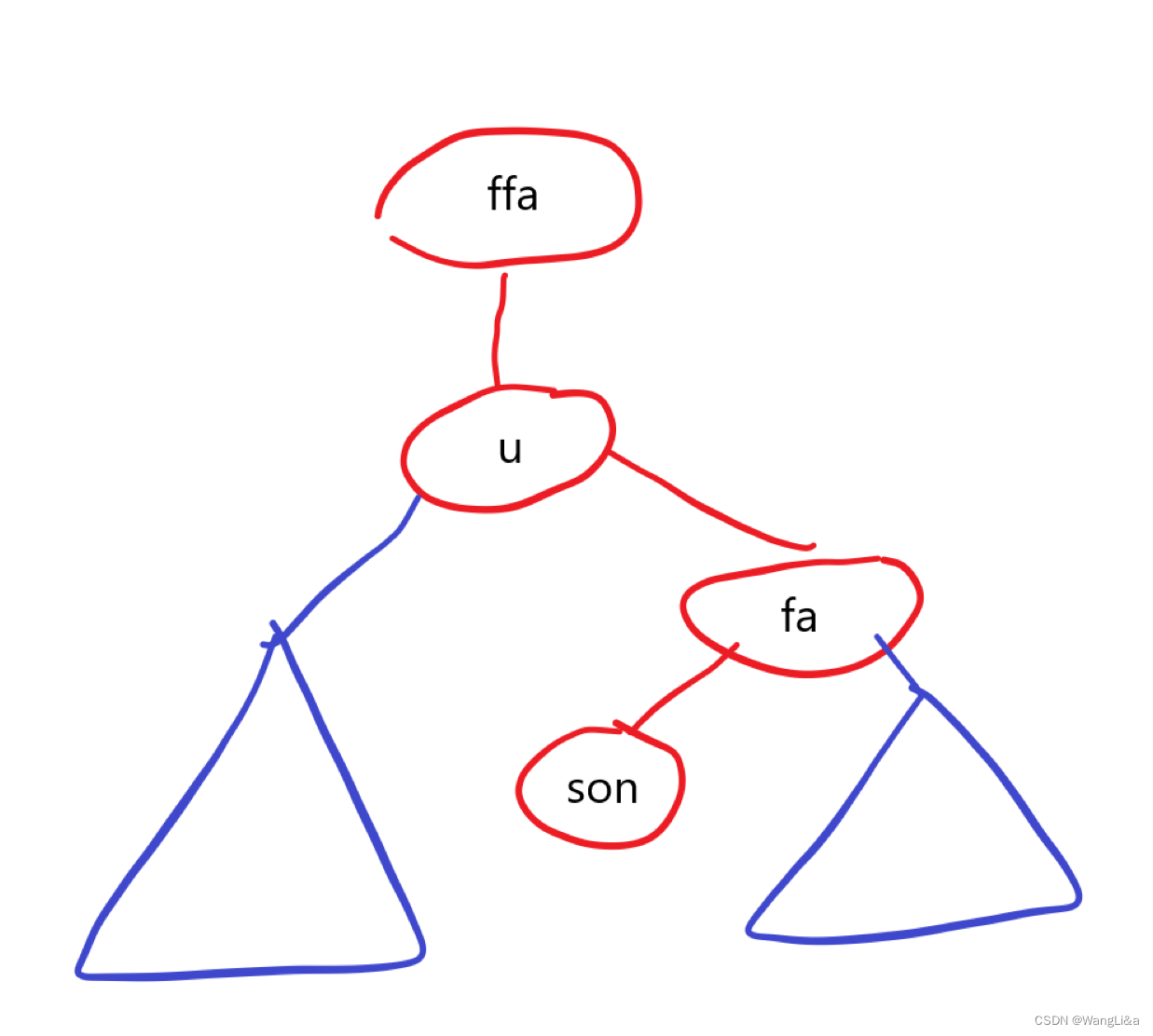
在这里插入图片描述

直接背下来写得比较快。

旋转实现

完整代码是这样的：

void rotate(int u) {int k=get(u),son=t[u].ch[k^1],fa=t[u].fa,ffa=t[fa].fa;add(ffa,u,get(fa));add(u,fa,k^1);add(fa,son,k);push_up(fa);push_up(u);
}

注意最后要更新节点信息。先push_up父亲，再push_up自身，因为此时，原来的父亲是自身的儿子。

保证编号为u的节点存在父亲。
（事实上，可能会有son=0或ffa=0，使得编号为0的节点可能携带有额外的祖先/后代信息，但是这不影响。）

其实我们还可以选择把子孙转成指定祖先的儿子处就停止，这里不多说了。

伸展（splay）

函数原型：

int splay(int);

伸展操作是执行若干次旋转操作，把编号为u的节点旋转到根，并返回u的编号。

执行的方法是这样的：

记录当且节点的编号u，更新它目前的父亲编号fa=t[u].fa，注意u的父亲是不断变化的，因此要更新：

如果u没有父亲，说明u是根节点：停止
如果fa不存在父亲，说明u再旋转一次就会旋转到根：rotete(u)
get(fa)==get(u)，说明u和fa是同侧儿子，先旋转fa，再旋转u：rotate(fa),rotate(u)
get(fa)!=get(u)，说明u和fa是异侧儿子，旋转两次u：rotate(u),rotate(u)

写成代码是这样的：

int splay(int u) {for(int fa; (fa=t[u].fa); rotate(u))if(t[fa].fa)rotate(get(u)==get(fa)?fa:u);return root=u;
}

注意最后把根节点编号设为u。

伸展主要有三个作用：

可以保证时间复杂度
rotate内有push_up函数，如果修改了u的信息，伸展一下可以更新到根节点的链上信息
把u旋转到根便于下一步操作

加入值（push）

函数原型：

int push(int);

函数push(val)将val在集合中出现的次数增加1，并返回val所在的节点编号，如果val在集合中原来并不存在，就创建一个新节点。

函数分为三种情况讨论：

Splay为空：直接新建一个节点，然后把根设为这个节点。
Splay中以前存在val这个值：找到存储这个值的节点，先把它旋转到根，然后把它的cnt增加1，再push_up以更新信息。
（因为此时这个节点已经是根了，对它调用splay不会rotate，因此必须手动psuh_up。
即使我们先前不把这个节点旋转到根，但是这个节点可能原本就是根，还是需要更新一下siz信息）
Splay中不存在val这个值：找到一个合适的叶子节点，然后对val新建一个节点，并且把新节点的父亲设为这个叶子节点。把这个节点旋转到根。

为了保证时间复杂度，同时为了更新链上记录的siz信息，最后都要把val所在的节点旋转到根。

函数定义：

int push(int val) {if(!root) {t[++tot].set(val);return root=tot;}int x=val_find(val);这里的val_find函数很特殊，如果找到val，会返回这个节点作为根节点，否则会返回一个可以作为新节点父亲的叶子节点if(t[x].val==val) {t[x].cnt++;push_up(x);return x;}t[++tot].set(val);要先set再加边，否则set会将t[tot]上存储的祖先/子孙信息清除add(x,tot,t[x].val<val);return splay(tot);
}

删去值（pop）

函数原型：

void pop(int);

函数pop(val)将集合中val出现的次数减1，保证val之前至少出现过一次。

函数分几种情况讨论：
首先找到val所在的节点的编号，设为u，然后把这个节点旋转到根。

如果t[u].cnt>1：直接让cnt--
如果u至少没有一个儿子，那就把根设为它的另一个儿子，然后删除u。
（如果u没有任何一个儿子是不影响的。）
否则，说明u既有左儿子，又有右儿子，也就是说val既有前驱又有后继：
因此找到val的前驱，把前驱旋转到根，此时u一定是根的右儿子，而且由于根是前驱，所以u没有左儿子，因此直接把u的右儿子设为根的右儿子，然后删除u即可。

注意最后要push_up(root)，因为第1,3种情况下需要更新根节点信息。

函数实现：

void pop(int val) {int u=val_find(val);if(t[u].cnt>1) t[u].cnt--;else if(!t[u].l||!t[u].r) root=t[u].l|t[u].r,del(u);else {pre(val);int r=t[u].r;del(u);这里要先清除u，再连边。否则清除u时会顺便擦除根节点和r节点的祖先关系信息add(root,r,1);此时前驱是根节点，把u的右儿子设为其前驱的右儿子}push_up(root);
}

用值查找（val_find）

函数原型：

int val_find(int);

函数val_find(val)在集合中查找值val，如果它出现过，那就把val所在的节点旋转到根，并且返回它的编号，如果它没有出现过，那就返回一个可以作为val父亲的叶子节点编号。
（如果此时树为空，函数会返回0，尽管不会出现这样的调用）

主要做法就是从根节点开始找，如果找到了就返回，没找到就按照大小关系继续往下走。
如果找到叶子节点还没找到val就返回它的父亲。

函数定义：

int val_find(int val) {int u=root,fa=0;while(u)if(t[fa=u].val==val) return splay(u);else u=t[u].ch[t[u].val<val];return fa;
}

用排名查找（rank_find）

函数原型：

int rank_find(int,int);

函数rank_find(u,rank)查找u子树内排名为rank的节点，并返回节点编号。注意这里是子树内排名，而不是全局排名。

我们通常调用时参数u=root，即查询全局排名。
把rank_find函数设计为两个参数，一方面是为了方便递归调用，另一方面，不为其提供一个参数的重载版本是为了防止将其与val_find函数与find_rank函数混淆。

rank_find(u,rank)函数这样设计：
分情况讨论：

如果rank<=左子树大小，递归到左儿子：rank_find(t[u].l,rank)
否则，如果rank>左子树大小+自身节点的cnt，递归到右儿子：rank_find(t[u].r,rank-t[t[u].l].siz-t[u].cnt)
否则：旋转并且返回自身节点编号

这种独特的递归顺序使得如果查询的rank大于子树之内的最大排名，会返回子树最大值的节点编号，避免了进一部的分情况讨论。

函数定义：

int rank_find(int u,int rank) {int l=t[t[u].l].siz;这样可以少打很多字if(rank<=l) return rank_find(t[u].l,rank);else if(rank>l+t[u].cnt) return rank_find(t[u].r,rank-l-t[u].cnt);return splay(u);
}

查询值的排名（find_rank）

函数原型：

int find_rank(int);

函数find_rank(val)查询值val的排名，不保证val出现过。
没有提供查询节点排名的函数是因为节点不存在排名，如果想要查询节点u对应的权值的排名，可以调用find_rank(t[u].val)。

查询val的排名，可以通过把val加入集合一次，然后把它对应的节点旋转到根。那么val的排名就是它对应节点的左子树的大小+1。
然后再把val在集合中删去一次。

函数定义：

int find_rank(int val) {int ans=t[t[push(val)].l].siz+1;pop(val);return ans;
}

查找前驱/后继（bound）

函数原型：

int bound(int,bool);

函数bound(val,k)用于查询前驱/后继，旋转节点到根，并返回对应的节点编号。
函数bound(val,0)用于查询值val的前驱。
函数bound(val,1)用于查询值val的后继。

bound原理

这里以查询前驱举例：
查询val前驱的方法就是，无论Splay中是否存在val，我们都先push(val)，这样Splay内肯定存在val，且为Splay的根。
走到根的左儿子上，然后不断地走右儿子，直到走到叶子节点即为前驱，记录答案后pop(val)。

查询后继的方法是类似的：先push(val)，走到根的右儿子上，然后不断地走左儿子，叶子节点即为前驱，记录答案后pop(val)。

注意到可以把这两种情况合并起来：设k=0表示查询前驱，k=1表示查询后继，则函数定义如下：

int bound(int val,bool k) {int u=t[push(val)].ch[k];while(t[u].ch[k^1]) u=t[u].ch[k^1];pop(val);return splay(u);
}

前驱（pre）

函数原型：

int pre(int);

pre为查询前驱提供了专门的接口。
函数pre(val)表示查询val的前驱，把前驱旋转到根，并且返回前驱编号。

val可以比集合中的任何数都要大，但是不能没有前驱，否则运行可能出现问题，我们没有保证splay(0)不会出错，因为我们没有保证t[0]不携带非零的祖先后代信息。

如果非要这样查询可能没有前驱/后继的数的话可以设置哨兵：push(-INF),push(INF)

函数定义：

int pre(int val) {return bound(val,0);
}

后继（nxt）

函数原型：

int nxt(int);

函数nxt(val)表示查询val的后继，把后继旋转到根，并返回后继编号。
必须要保证val有后继。

函数定义：

int nxt(int val) {return bound(val,1);
}

完整代码

空间复杂度

注意到Splay的任意一种操作至多创建一个节点，因此空间复杂度为一倍操作次数。（本题要算上一开始的 $10^5$ 次操作）

代码

#include<iostream>
using namespace std;
const int N=2e6;
struct node {int fa,ch[2];int val,cnt,siz;int &l=ch[0],&r=ch[1];void set(int v,int c=1,int s=1) {l=r=fa;val=v;cnt=c;siz=s;}
}t[1100005];
int tot,root;
bool get(int);
void push_up(int);
void add(int,int,bool);
void del(int);
void rotate(int);
int splay(int);
int push(int);
void pop(int);
int val_find(int);
int rank_find(int,int);
int find_rank(int);
int bound(int,bool);
int pre(int);
int nxt(int);
int a[N+5];
int main() {int n,m;cin>>n>>m;for(int i=1;i<=n;i++) cin>>a[i];for(int i=1;i<=n;i++) push(a[i]);int ans=0,last=0;while(m--) {int op,x;cin>>op>>x;
//		if(op==1) push(x);
//		if(op==2) pop(x);
//		if(op==3) cout<<find_rank(x)<<endl;
//		if(op==4) cout<<t[rank_find(root,x)].val<<endl;
//		if(op==5) cout<<t[pre(x)].val<<endl;
//		if(op==6) cout<<t[nxt(x)].val<<endl;x^=last;if(op==1) push(x);if(op==2) pop(x);if(op==3) ans^=(last=find_rank(x));if(op==4) ans^=(last=t[rank_find(root,x)].val);if(op==5) ans^=(last=t[pre(x)].val);if(op==6) ans^=(last=t[nxt(x)].val);}cout<<ans;
}
bool get(int u) {return t[t[u].fa].r==u;
}
void push_up(int u) {t[u].siz=t[t[u].l].siz+t[t[u].r].siz+t[u].cnt;
}
void add(int fa,int son,bool k) {t[t[son].fa=fa].ch[k]=son;
}
void del(int u) {t[t[u].l].fa=t[t[u].r].fa=t[t[u].fa].ch[get(u)]=0;t[u].set(0,0,0);
}
void rotate(int u) {int k=get(u),son=t[u].ch[k^1],fa=t[u].fa,ffa=t[fa].fa;add(ffa,u,get(fa));add(u,fa,k^1);add(fa,son,k);push_up(fa);push_up(u);
}
int splay(int u) {for(int fa;(fa=t[u].fa);rotate(u)) if(t[fa].fa)rotate(get(fa)==get(u)?fa:u);return root=u;
}
int push(int val) {if(!root) {t[++tot].set(val);return root=tot;}int x=val_find(val) ;if(t[x].val==val) {t[x].cnt++;push_up(x);return x;}t[++tot].set(val);add(x,tot,t[x].val<val);return splay(tot);
}
void pop(int val) {int u=val_find(val);if(t[u].cnt>1) t[u].cnt--;else if(!t[u].l||!t[u].r) root=t[u].l|t[u].r,del(u);else {pre(val);int r=t[u].r;del(u);add(root,r,1);}push_up(root);
}
int val_find(int val) {int u=root,fa=0;while(u) if(t[fa=u].val==val) return splay(u);else u=t[u].ch[t[u].val<val];return fa;
}
int rank_find(int u,int rank) {int l=t[t[u].l].siz;if(rank<=l) return rank_find(t[u].l,rank);else if(rank>t[u].cnt+l) return rank_find(t[u].r,rank-t[u].cnt-l);return splay(u);
}
int find_rank(int val) {int ans=t[t[push(val)].l].siz+1;pop(val);return ans;
}
int bound(int val,bool k) {int u=t[push(val)].ch[k];while(t[u].ch[k^1]) u=t[u].ch[k^1];pop(val);return splay(u);
}
int pre(int val) {return bound(val,0);
}
int nxt(int val) {return bound(val,1);
}