重庆开县网站建设公司百度推广找谁
重建二叉树
- 一、递归法
- 二、迭代法
题目链接
题目描述:
输入某二叉树的前序遍历和中序遍历的结果,请构建该二叉树并返回其根节点。
假设输入的前序遍历和中序遍历的结果中都不含重复的数字。
示例 1:

Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
示例 2:
Input: preorder = [-1], inorder = [-1]
Output: [-1]
一、递归法
首先我们知道中序的左边就是该节点的左子树,中序的右边就是该节点的右子树,而确认根的顺序就需要靠前序。
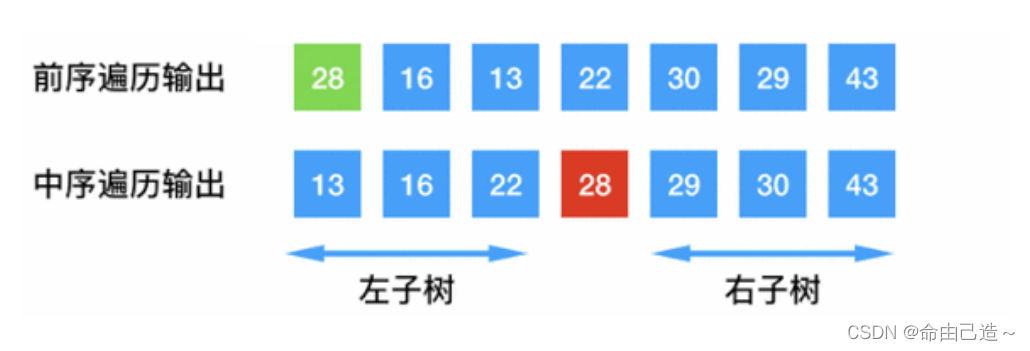
所以我们可以用一个变量pi记录前序遍历的位置,在中序中找到相同的元素,然后把它的左右区间递归下去。
这里注意如果要每次递归都需要遍历中序找到根,时间复杂度过高,所以我们可以在递归前先用哈希表映射根的位置。
代码如下
class Solution {
public:unordered_map<int, int> index;TreeNode* _bulidTree(vector<int>& pre, vector<int>& in, int& pi, int begin, int end){if (begin > end) return nullptr;int mid = index[pre[pi]];TreeNode* root = new TreeNode(pre[pi++]);root->left = _bulidTree(pre, in, pi, begin, mid - 1);root->right = _bulidTree(pre, in, pi, mid + 1, end);return root;}TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {int pi = 0;for (int i = 0; i < preorder.size(); i++){index[inorder[i]] = i;}return _bulidTree(preorder, inorder, pi, 0, preorder.size() - 1);}
};
二、迭代法
三种顺序的迭代法遍历:【数据结构】二叉树的非递归遍历
我们先假象一种情况,一棵树只有左子树的话,那么就相当于是一个单链表,那么它的前序遍历和中序遍历就刚好是反过来的。那么我们就可以使用栈来逆序存放,一旦遍历到最左下节点,这时候就该返回,开始弹栈,当我们发现弹栈的顺序和中序遍历不一致的时候,说明最后一个弹出来的节点有右子树。
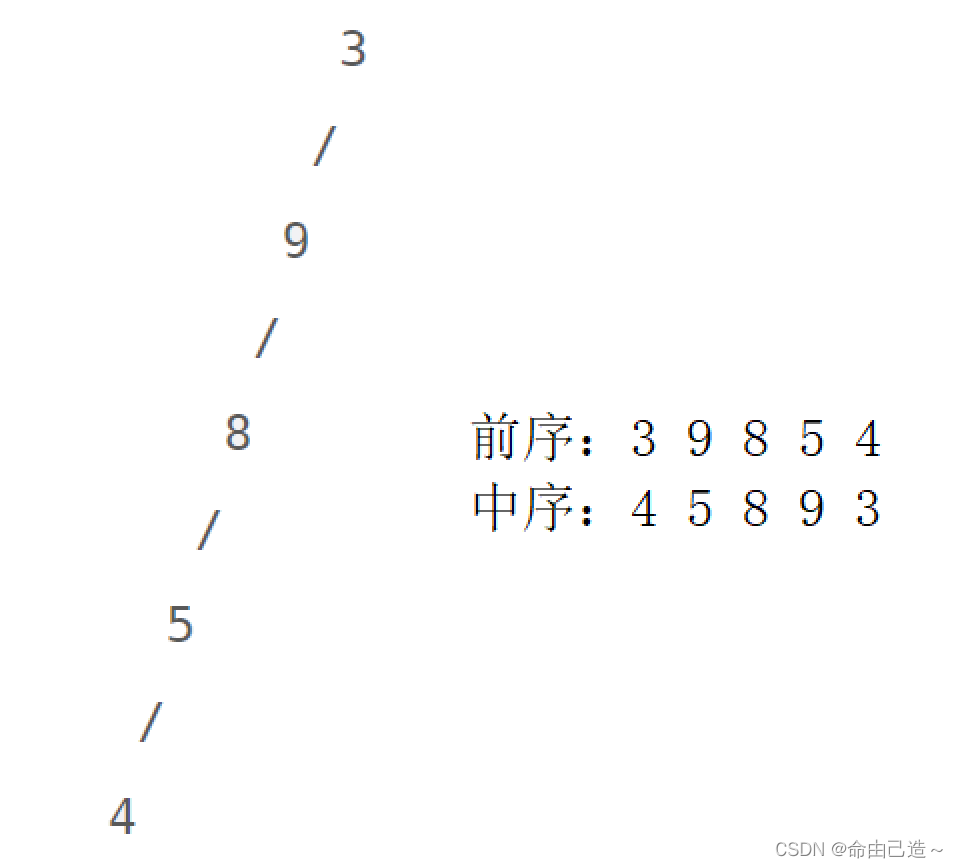
可以发现前序走完后出栈顺序刚好是中序遍历的结果,所以没有右子树。
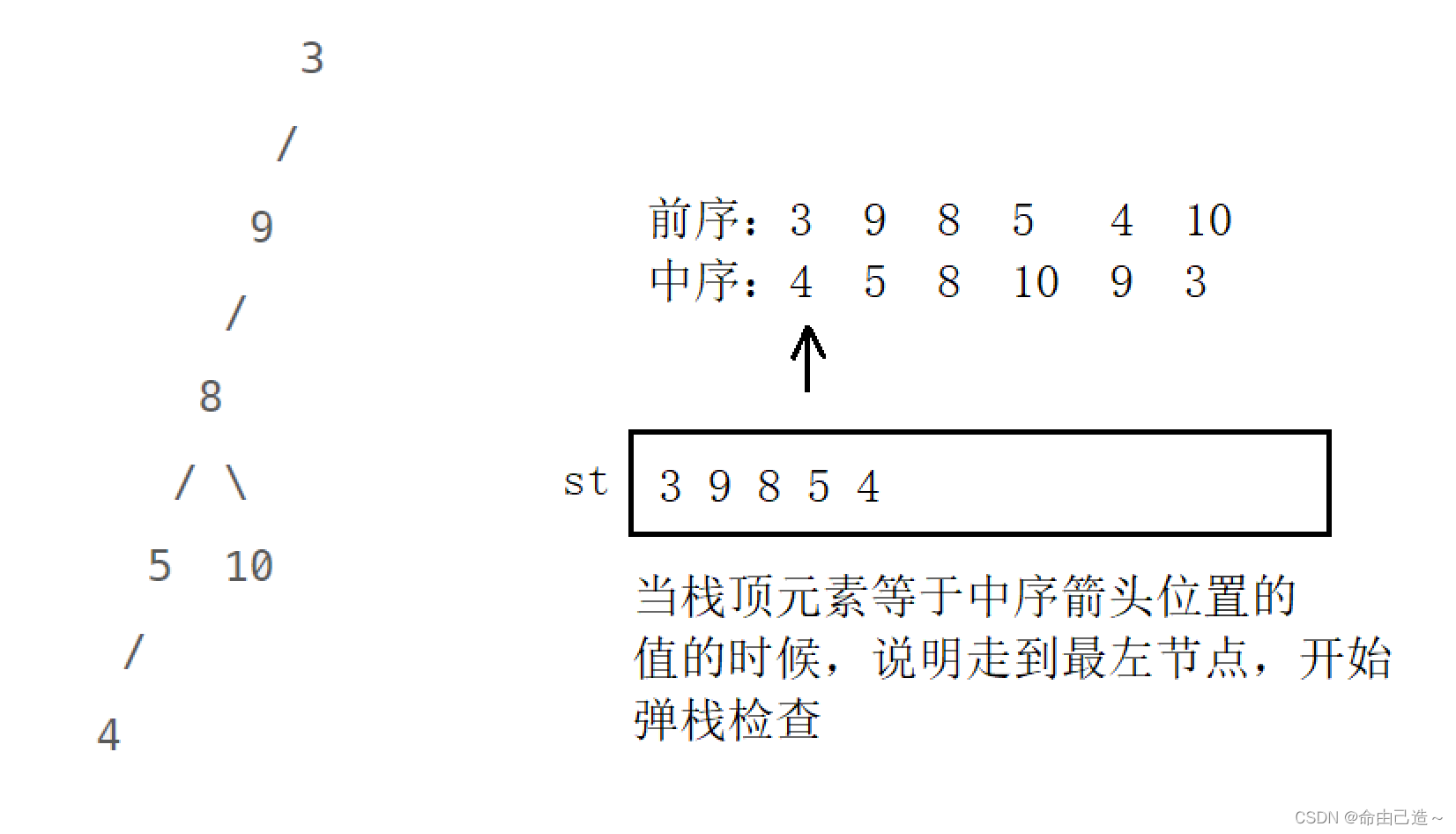
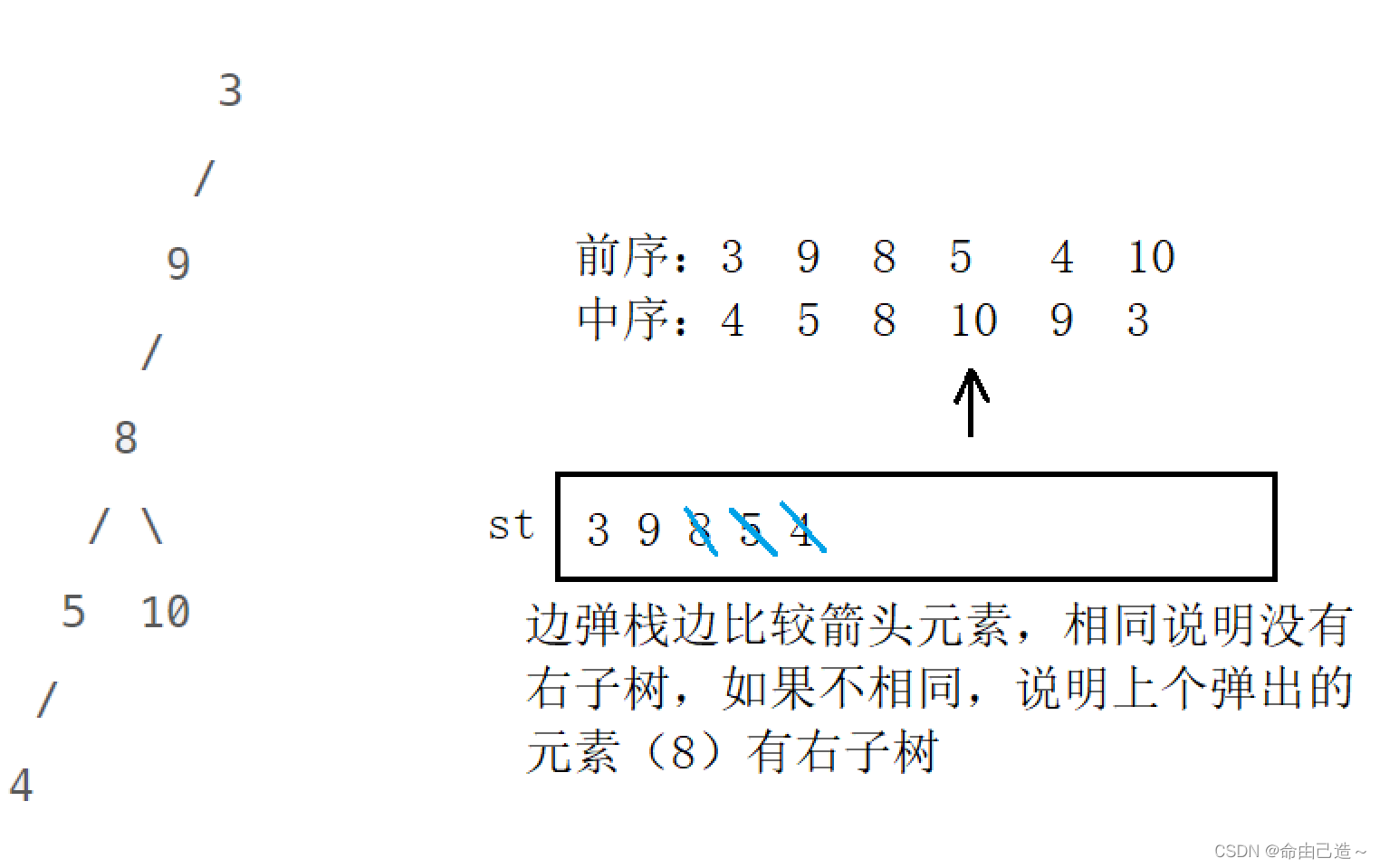
代码如下:
class Solution {
public:TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {if(preorder.empty()) return nullptr;stack<TreeNode*> st;int inorIndex = 0;TreeNode* root = new TreeNode(preorder[0]);st.push(root);for(int i = 1; i < preorder.size(); i++){TreeNode* node = st.top();if(node->val != inorder[inorIndex]){node->left = new TreeNode(preorder[i]);st.push(node->left);}else{while(!st.empty() && st.top()->val == inorder[inorIndex]){node = st.top();st.pop();inorIndex++;}node->right = new TreeNode(preorder[i]);st.push(node->right);}}return root;}
};
