做的好的办公家具网站谷歌优化seo

一.二叉树的顺序结构

1.定义：使用数组存储数据，一般使用数组只适合表示完全二叉树，此时不会有空间的浪费

注：二叉树的顺序存储在逻辑上是一颗二叉树，但是在物理上是一个数组，此时需要程序员自己想清楚调整数据时应该怎样调整

2.堆

(1)定义：集合中所有元素按照完全二叉树的顺序存储在一个一维数组中，并满足Ki<=K2*i+1且K2*i+2(或Ki<=K2*i+1且K2*i+2)的规律，则称之为堆

(2)性质：

1>堆中某个节点的值总是不大于(或不小于)其父节点的值

2>堆是一颗完全二叉树

3>大堆：任何一个父节点的值>=孩子的值

    小堆：任何一个父节点的值<=孩子的值

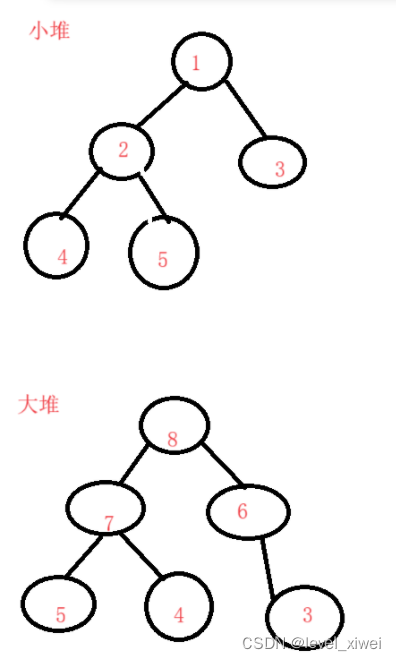
(3)堆的实现(以小堆为例)

1>堆的结构体定义：数组指针(用于存储数据),有效数据个数，空间容量大小

typedef int HeapDataType;
typedef struct Heap
{HeapDataType* a;//数组指针int size;//有效数据个数int capacity;//有效空间大小
}HP;

2>堆的初始化：

//堆的初始化
void HPInit(HP* ph)
{assert(ph);ph->a = NULL;ph->size = ph->capacity = 0;
}

3>堆的销毁：

//堆的销毁
void HPDestory(HP* ph)
{assert(ph);free(ph->a);ph->a = NULL;ph->size = ph->capacity = 0;
}

4>向堆中插入数据：

**思路：将数据插在原数据的最后面，在不断向上调整以保证插入数据后仍为小堆 

**画图解释

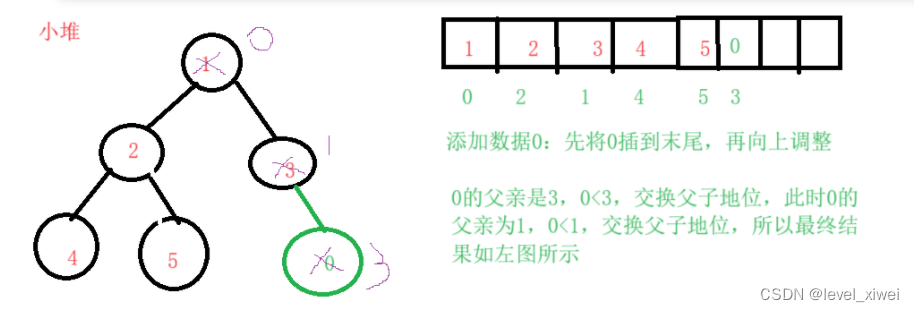
**代码实现

//向堆内插入数据
void HPPush(HP* ph, HeapDataType x)
{assert(ph);//判断是否需要增容if (ph->size == ph->capacity){int newcapacity = ph->capacity * 2 == 0 ? 4 : ph->capacity * 2;HeapDataType* tmp = (HeapDataType*)realloc(ph->a, sizeof(HeapDataType) * newcapacity);if (tmp == NULL){perror("realloc fail");return;}ph->a = tmp;ph->capacity = newcapacity;}ph->a[ph->size] = x;ph->size++;AdjustUp(ph->a, ph->size-1);}

5>向上调整数据：

思路：找孩子的父亲，判断父亲是否大于孩子，若大于则交换父子地位，继续向上调整

 注：由于堆是完全二叉树，一个父亲最多有两个孩子，所以父亲的下标应该是孩子的下标减一再除以2，即parent=(child-1)/2;

//向上调整
void AdjustUp(HeapDataType* a, int child)
{int parent = (child - 1) / 2;while (child > 0){if (a[parent] > a[child]){Swap(&a[parent], &a[child]);child = parent;parent= (child - 1) / 2;}else{break;}}
}

6>删除根部数据：

思路：先交换根部数据和最后一个数据，再删除根部数据，同时将最后一个数据向下调整以保证删除后的堆仍为小堆

//删除堆顶数据(根位置)
void HPPop(HP* ph)
{assert(ph);Swap(&ph->a[0], &ph->a[ph->size - 1]);ph->size--;AdjustDown(ph->a, ph->size, 0);
}

7>向下调整数据：

**思路：先找左右孩子中较小的那个孩子，与父亲相比，若父亲大于孩子，则交换父子地位，继续向下调整

注：由于堆是完全二叉树，一个父亲最多有两个孩子，所以左孩子的下标应该是父亲的下标乘以2再加1，即child=parent*2+1;

**画图解释

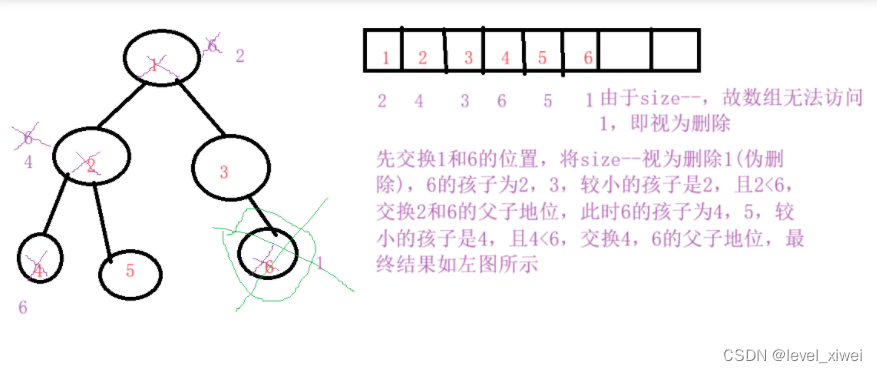
**代码实现

//向下调整
void AdjustDown(HeapDataType* a, int size, int parent)
{//默认左孩子小int child = parent * 2 + 1;while (child < size){//找左右孩子中小的那一个if ((child+1) < size && a[child+1] < a[child]){child ++;}if (a[parent] > a[child]){Swap(&a[parent], &a[child]);parent = child;child = parent * 2 + 1;}else{break;}}
}

(4)堆的应用

1>堆排序

1.1)思路：注：降序：建小堆，升序建大堆

             将数组中的元素建堆，交换最后的数据与首位数据，并进行向下调整，让size--，循环操                 作，直至完成排序

1.2)时间复杂度：O（N*log N）

1.3)画图解释：

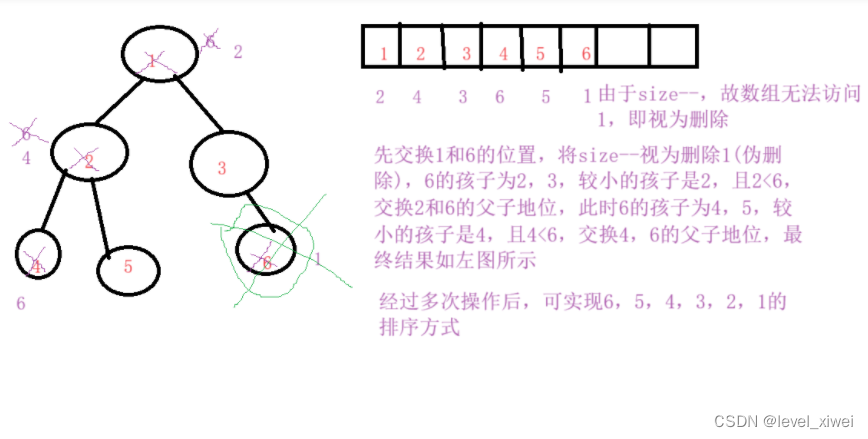
1.4)代码实现

void HeapSort(int* a, int size)
{//将数组建堆for (int i = 1; i < size; i++){AdjustUp(a, i);}int end = size - 1;while (end > 0){Swap(&a[0], &a[end]);AdjustDown(a, end, 0);--end;}
}

2>TOP_K(以求前K个最大的数据为例)

2.1)定义：求出数据中前K个最大的数据（或前K个最小的数据）

2.2)思路：

思路一：创建一个含N个节点的大堆，PopK次，即可获取前K个最大的数据

              弊端：当N非常大时，在创建节点时需要占用大量的内存

思路二：建一个含K个节点的小堆，将剩余的N-K个数据与堆顶数据相比，若大于堆顶数据则入                    堆进行向下调整，否则进行下一个比较

注：思路二更优，效率高

2.3)代码实现

void TOP_K(int* a,int n,int k) 
{//在文件中读取数据const char* fp = "data.txt";FILE* fout = fopen(fp, "r");if (fout == NULL){perror("fopen fail");return;}//读取前K个数据for (int i = 0; i < k; i++){fscanf(fout,"%d", &a[i]);}//建小堆for (int i = (k-1-1)/2;i>=0;i--){AdjustDown(a, k, i);}//将剩余的n-k个数据于堆顶数据相比int x = 0;while (fscanf(fout,"%d",&x)!=EOF){if (a[0]<x){a[0] = x;AdjustDown(a, k, 0);}}for (int i = 0; i < k; i++){printf("%d ", a[i]);}printf("\n");
}

2.4)数据验证

思路：将N的节点的数据模上N，是他们处于小于N的状态，在随机挑K个数据将他们调大于N，若在选出来的K个数据为大于N的数据，则说明该程序执行的是选取前K个最大的数据的指令

二.二叉树的链式结构(以二叉链表为例)

注：在二叉树的实现中多用递归来达到一层一层向下查找的目的(所以读者需要熟练掌握递归的相关知识)

1.定义：用链表表示一颗二叉树，即用链表表示元素之间的逻辑关系

2.二叉树节点的定义：该节点内存储的数据，指向左孩子的指针，指向右孩子的指针

typedef int BTNodeData;
typedef struct BinaryTreeNode
{BTNodeData val;struct BinaryTreeNode* left;struct BinaryTreeNode* right;
}BTNode;

3.二叉树的创建(根据前序遍历来创建二叉树)：

以数组abd##e#h##cf##g##构建二叉树

1>思路：1)若当前数据为#，则返回NULL；

               2)否则开辟一个二叉树节点root，将该数据赋给val,给左，右孩子赋值，通过调用函数递                 归实现

2>代码实现：

//创建二叉树
BTNode* BTCreate(BTNodeData* a, int* pi)
{if (a[*pi] == ‘#’){(*pi)++;return NULL;}BTNode* root = (BTNode*)malloc(sizeof(BTNode));root->val = a[*pi];(*pi)++;root->left = BTCreate(a,pi);root->right = BTCreate(a, pi);return root;
}

4.二叉树的前序遍历：

1>访问顺序：根，左子树，右子树

2>思路：如果根为空，打印N，什么都不返回；否则先打印根的值，再调用该函数，将左子树的地址作为参数，然后调用该函数，将右子树的地址作为参数，利用递归实现前序遍历

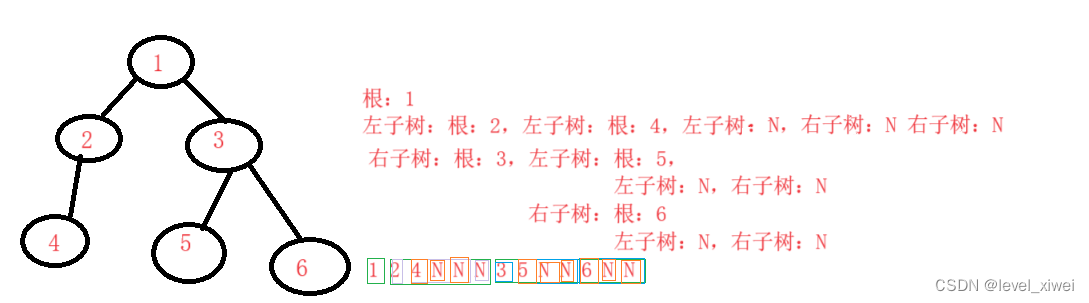
3>代码实现

//前序遍历
void PreOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}printf("%d ", root->val);PreOrder(root->left);PreOrder(root->right);
}

5.二叉树的中序遍历

1>访问顺序：左子树，根，右子树

2>思路：与前序遍历类似

3>代码实现

//中序遍历
void InOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}InOrder(root->left);printf("%d ", root->val);InOrder(root->right);
}

6.二叉树的后序遍历

1>访问顺序：左子树，右子树，根

2>思路：与前序遍历类似

3>代码实现

//后序遍历
void PostOrder(BTNode* root)
{if (root == NULL){printf("N ");return;}PostOrder(root->left);PostOrder(root->right);printf("%d ", root->val);
}

7.二叉树的层序遍历

1>思路：利用队列，让上一层的节点先入队列，在删除他们时，带进去下一层，若节点为空不进队列

2>代码实现：

//层序遍历
void BTLevelOrder(BTNode* root)
{Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);printf("%d ", front->val);//当节点不为空时入队列if (front->left){QueuePush(&q, front->left);}if(front->right){QueuePush(&q, front->right);}}printf("\n");QueueDestory(&q);
}

8.二叉树的节点个数

1>思路：1)如果根节点为空，返回0；

               2)否则返回左子树的节点数+右子树的节点数+1(利用递归法实现左右子树节点数的计算)

2>代码实现：

//二叉树节点个数
int BTSize(BTNode* root)
{if (root == NULL){return 0;}return  BTSize(root->left) + BTSize(root->right) + 1;
}

9.二叉树的叶子节点个数

1>思路：1)如果根为空，返回0；

               2)如果左右孩子均为空，返回1；

               3)否则返回左子树叶子数+右子树叶子数(利用递归实现左右子树叶子数的计算)

2>代码实现：

//二叉树叶子节点个数
int BTLeafSize(BTNode* root)
{if (root == NULL){return 0;}if (root->left == NULL && root->right == NULL){return 1;}return BTLeafSize(root->left) + BTLeafSize(root->right);
}

10.二叉树第K层节点个数

1>思路：1)如果根为空返回0；

               2)如果k==1，返回1；

               3)否则返回左子树的k-1层+右子树的k-1层

注：将树一层一层向下压，直至出现两种特殊情况

2>代码实现：

//二叉树第K层节点个数
int BTLevelKSize(BTNode* root, int k)
{if (root == NULL){return 0;}if (k == 1){return 1;}return BTLevelKSize(root->left, k - 1) + BTLevelKSize(root->right, k - 1);
}

11.二叉树查找值为X的节点

1>思路：1)若根为空，返回空；

               2)若根的值等于待查找数据，返回根的地址；

              3)否则查找左子树是否有值为X的节点若有返回该节点的地址，否则查找右子树是否有值                  为X的节点若有返回该节点的地址，若左右子树均没有是否有值为X的节点，则返回空

2>代码实现：

//二叉树查找值为X的节点
BTNode* BTFind(BTNode* root, BTNodeData x)
{if (root == NULL){return NULL;}if (root->val == x){return root;}//比较左子树是否有节点值为xBTNode* ret1 = BTFind(root->left, x);if (ret1!=NULL){return ret1;}//比较右子树是否有节点值为xBTNode* ret2 = BTFind(root->right, x);if (ret2 != NULL){return ret2;}//左右子树中均未找到值为x的节点return NULL;
}

12.树的高度

1>思路：1)若根为空，返回0；

               2)否则记录并分别求左右子树的高度，哪个值更大哪个即为树的高度

注：每次都需记录所求的树的高度，否则会出现走到上一层忘了下一层的情况，导致反复求某棵树高度的情况

2>代码实现：

//二叉树的高度
int BTHeight(BTNode* root)
{if (root == NULL){return 0;}int HeightLeft = BTHeight(root->left)+1;int HeightRight = BTHeight(root->right)+1;return HeightLeft > HeightRight ? HeightLeft  : HeightRight ;
}

13.二叉树的销毁

1>思路：用后序遍历的思想先销毁左右子树，再销毁根(若先销毁根，销毁根后，无法找到左右子树)

2>代码实现

//二叉树的销毁
void BTDestory(BTNode* root)
{if (root == NULL)return;BTDestory(root->left);BTDestory(root->right);free(root);}

14.判断二叉树是否为完全二叉树

1>思路：无论节点是否为空都入队列，当检查到第一个空节点时，开始遍历后面的节点看是否有非空节点，若有，则不是完全二叉树，否则是完全二叉树

2>代码实现

//二叉树是否为完全二叉树
bool BTComplete(BTNode* root)
{Queue q;QueueInit(&q);if (root){QueuePush(&q, root);}while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);//若第一个空如队列，跳出循坏，开始遍历看之后是否有非空节点的存在if (front == NULL){break;}QueuePush(&q, front->left);QueuePush(&q, front->right);}//遍历，看是否有非空节点while (!QueueEmpty(&q)){BTNode* front = QueueFront(&q);QueuePop(&q);if (front != NULL){QueueDestory(&q);return false;}}QueueDestory(&q);return true;
}