263企业邮箱官方入口网页版seo排名优化是什么意思

对于三种遍历方式来说，均为先左后右！区别在于根结点的位置顺序

先序遍历：根——左——右

中序遍历：左——根——右

后序遍历：左——右——根

（所谓先中后的顺序，是指根结点D先于子树还是后于子树出现）

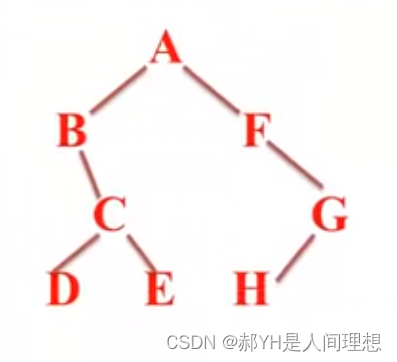
 如上图：

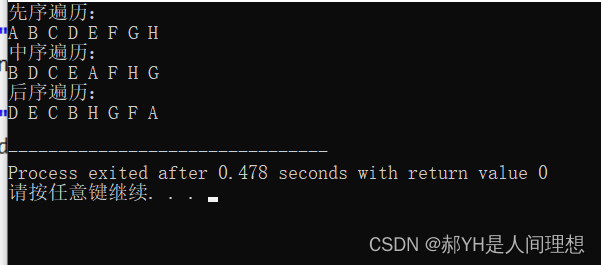
先序遍历的结果为：A B C D E F G H

中序遍历的结果为：B D C E A F H G

后序遍历的结果为：D E C B H G F A

---

定义树的结点类型

typedef struct BinaryNode{char ch;struct BinaryNode* lchild;struct BinaryNode* rchild;
}BinaryNode;

根据图例创建二叉树

void CreateBinaryTree()
{//创建结点 BinaryNode node1={'A',NULL,NULL};BinaryNode node2={'B',NULL,NULL};BinaryNode node3={'C',NULL,NULL};BinaryNode node4={'D',NULL,NULL};BinaryNode node5={'E',NULL,NULL};BinaryNode node6={'F',NULL,NULL};BinaryNode node7={'G',NULL,NULL};BinaryNode node8={'H',NULL,NULL};//创建结点关系node1.lchild=&node2;node1.rchild=&node6;node2.rchild=&node3;node3.lchild=&node4;node3.rchild=&node5;node6.rchild=&node7;node7.lchild=&node8;
}

递归实现先序遍历

void RecursionFirst(BinaryNode* root)
{ if(root==NULL)//遍历到空结点return;cout<<(root->ch)<<" "; //输出根结点RecursionFirst(root->lchild);//要点：虽然一左一右看似连在一起，其实是将首个根结点的左子树全部遍历完毕，才会去遍历右子树 RecursionFirst(root->rchild);//先序遍历的顺序为：根-左-右 	
}

递归实现中序遍历

void RecursionMiddle(BinaryNode* root)
{if(root==NULL)return;RecursionMiddle(root->lchild);cout<<(root->ch)<<" "; RecursionMiddle(root->rchild);//中序遍历的顺序为：左-根-右 	
}

递归实现后序遍历

void RecursionLast(BinaryNode* root)
{if(root==NULL)return;RecursionLast(root->lchild);RecursionLast(root->rchild);cout<<(root->ch)<<" "; //后序遍历的顺序为：左-右-根 
}

在CreateBinaryTree方法中添加函数调用

	//遍历结点cout<<"先序遍历："<<endl; RecursionFirst(&node1); cout<<endl; cout<<"中序遍历："<<endl; RecursionMiddle(&node1);cout<<endl; cout<<"后序遍历："<<endl; RecursionLast(&node1);cout<<endl; 

头文件及主函数

int main(int argc, char** argv) {CreateBinaryTree();//主函数只负责调用即可 return 0;
}

运行结果如下：与结果相一致