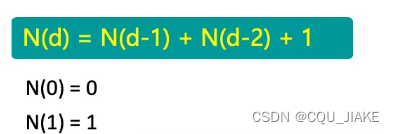一点一创平面设计seo关键词分析
完全二叉树结点的度可能有1,满二叉树的度只能为0或2
BST构建
BST是左孩子都比根节点小,右孩子都比根节点大
二叉搜索树的插入,删除,调整
平衡树理解
任何一个平衡二叉树,它的中序遍历都是一样的,都是有序的从小到大
之所以有调整,就是谁当根节点不同导致的。
作为根节点,就需要提供两个信息,一个是左孩子,一个是右孩子。
那么中序遍历的过程就是,先由根节点向左一直蔓延,直到到底,然后从左到右依次遍历,遍历到根节点,再从根节点向右遍历蔓延。想象一个有序序列,找到任意一个起点,这个起点就是所谓的树的根节点,那么中序遍历就是左根右,即从左到右,就是从起点(根节点)先一直向左,到底后再逐个输出,那就是中序序列。有这样的性质,就是因为左根右,序列中的每个结点左侧都是它的左孩子,它的右侧都是右孩子或者父母结点
即,左侧只会是左孩子,但右侧可能是右孩子或父母节点,但由于左孩子都小于根节点,所以一旦有右孩子,那么只能先是右孩子,即右孩子的优先级大于父母结点,因为右孩子一定小于父母节点。
AVL树
平衡因子是根节点的定义,即根节点的左右孩子高度差
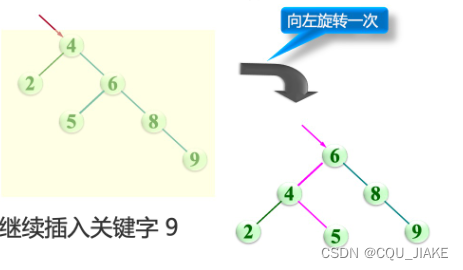
如这里是4的平衡因子不满足条件,其左子树,右子树高度差大于1
求高度函数
typedef struct node {int data;node* lchild, * rchild;
}*tree;
int high(tree root) {if (root) {return max(high(root->lchild), high(root->rchild)) + 1;}return 0;
}AVL树的构建
AVL树的调整
中序遍历都是一样的,不一样的就是根节点的确定,即起点的确定
右旋
右旋的具体步骤:
- T向右旋转成为L的右结点
- L的右节点Y 放到 T的左孩子上
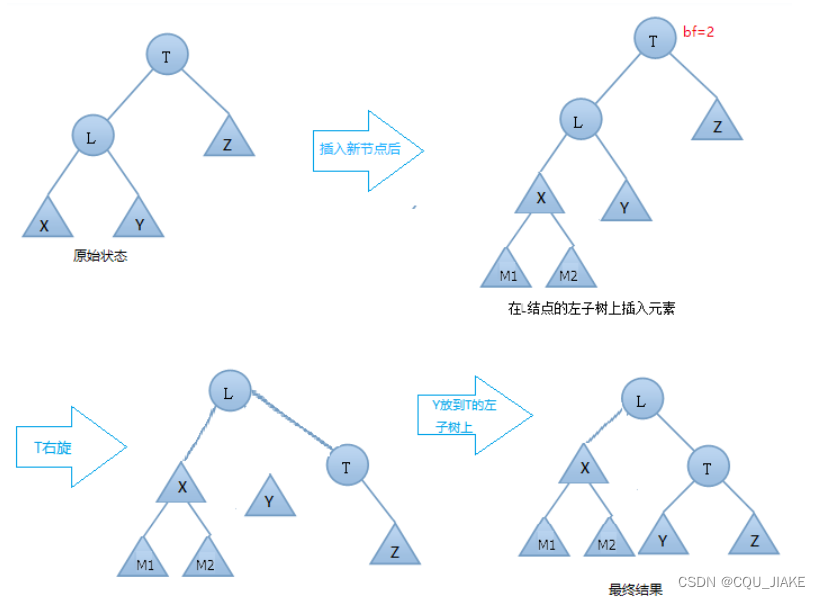
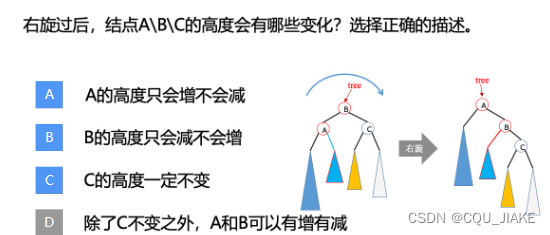
如何判断是否为AVL
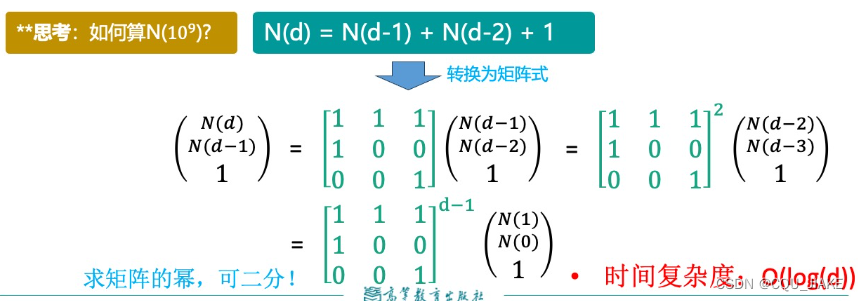
AVL树高度

由于AVL树的左右子树都是AVL树,
自变量是N,AVL树的高度。那么由于AVL树左右平衡,根节点平衡,所以对于高度为d的AVL树,根节点占一层,那么左子树(默认左子树高一点)高度为d-1,(此时加起来为d);右子树高度为d-2,因为要满足左右子树高度差不大于1而且结点要尽可能少,所以有