网站的数据库选择seo推广服务哪家好
目录
Trie树
并查集
堆
Trie树
作用:用来高效地存储和查找字符串集合的数据结构
基本形式:
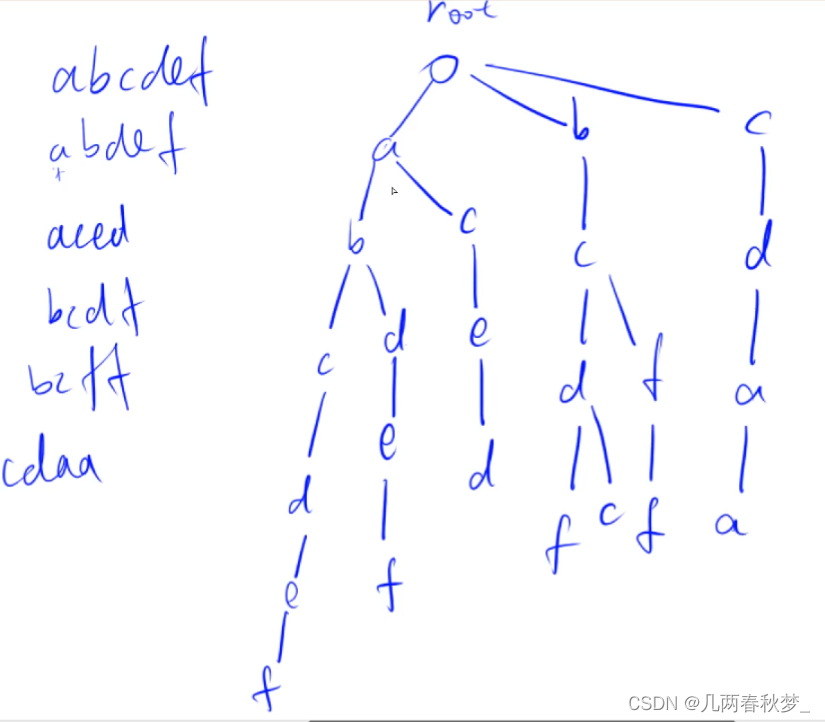
模板代码如下:
#include<iostream>
using namespace std;const int N = 100010;//idx代表当前用到哪个下标
//既是根节点,又是空节点
//cnt存储的是以当前点结尾的单词有多少
int son[N][26],cnt[N],idx;//插入
void insert(char str[])
{int p = 0;for(int i = 0;str[i];i++){int u = str[i] - 'a';if(!son[p][u]) son[p][u] = ++idx;p = son[p][u];}cnt[p] ++;
}//查询
int query(char str[])
{int p = 0;for(int i = 0;str[i];i++){int u = str[i] - 'a';if(!son[p][u]) return 0;p = son[p][u];}return cnt[p];
}并查集
1、将两个集合合并
2、询问两个元素是否在一个集合当中
基本原理:
用树的形式来维护集合。树根的编号就是整个集合的编号。每个节点存储它的父节点,p[x]表示x的父节点。
#include<iostream>
using namespace std;const int N = 100010;//father数组
int p[N];
int n,m;//返回x的祖宗节点
int find(int x)
{if(p[x] != x) p[x] = find(p[x]);return p[x];
}int main()
{scanf("%d%d",&n,&m);for(int i = 0;i<=n;i++) p[i] = i;while(m--){char op[2];int a,b;scanf("%s%d%d",op,&a,&b);if(op[0] == 'M') p[find(a)] = find(b); //将b的祖宗节点接到a的祖宗节点的下方else{if(find(a) == find(b)) puts("Yes");else{puts("No");}}}return 0;
}
堆
下面操作默认坐标为1开始
- 插入一个数 heap[++size] = x;up(size)
- 求集合中最小值 heap[1]
- 删除最小值 heap[1] = heap[size]; size--;down(1);
- 删除任意第k个元素 heap[k] = heap[size];size--; down(k);up(k);
- 修改任意一个元素 heap[k] = x;dwon(k);up(k);
#include<iostream>
using namespace std;const int N = 100010;int n,m;
int h[N],size;//down操作
void down(int u)
{int t = u;if(2*u <= size && h[2*u] < h[t]) t = 2*u;if(2*u +1 <= size && h[2*u +1] < h[t]) t = 2*u+1;if(u != t){swap(h[u],h[t]);down(t);}
}//up操作
void up(int u)
{while(u/2 && h[u/2] > h[u]){swap(h[u/2],h[u]);u /=2;}
}int main()
{scanf("%d",&n);for(int i =0;i<=n;i++) scanf("%d",&h[i]);size = n;for(int i = n/2;i;i--) down(i);while(m--){printf("%d",h[1]);//删掉堆顶h[1] = h[size];size --;down(1);}}