衡阳建设学校官方网站百度推广下载

目录
1. 列表奇偶拆分 ★
2. 二叉树的后序遍历 ★★
3. 接雨水 ★★★
附录
二叉树
特点
性质
特殊二叉树
满二叉树
完全二叉树
完全二叉树性质
二叉树的遍历
1. 列表奇偶拆分
【问题描述】 输入一个列表,包含若干个整数(允许为空),然后将其中的奇数和偶数单独放置在一个列表中,保持原有顺序
【输入形式】
【输出形式】
分两行输出,第一行输出偶数序列,第二行输出奇数序列
【样例输入1】
[48,82,47,54,55,57,27,73,86,14]
【样例输出1】
48, 82, 54, 86, 14
47, 55, 57, 27, 73
【样例输入2】
[10, 22, 40] 【
样例输出2】
10, 22, 40
NONE
【样例说明】
如果奇偶拆分后,奇数列表,或者偶数列表为空,请直接输出NONE表示
【代码】
x = input()
x1 = x.strip('[]')
x2 = x1.split(",")
a = []
b = []
for i in x2:if int(i) % 2 == 0:a.append(i)else:b.append(i)
if a == []:print("NONE")
else:print(a)
if b == []:print("NONE")
else:print(b)输入输出:
48,82,47,54,55,57,27,73,86,14
['48', '82', '54', '86', '14']
['47', '55', '57', '27', '73']
==============================
10, 22, 40
['10', ' 22', ' 40']
NONE
2. 二叉树的后序遍历
给定一个二叉树,返回它的 后序 遍历。
示例:
输入: [1,null,2,3] 输出: [3,2,1] 进阶: 递归算法很简单,你可以通过迭代算法完成吗?
代码:
class TreeNode:def __init__(self, x):self.val = xself.left = Noneself.right = None
class Solution(object):def postorderTraversal(self, root: TreeNode):if root is None:return []stack, output = [], []stack.append(root)while stack:node = stack.pop()output.append(node.val)if node.left:stack.append(node.left)if node.right:stack.append(node.right)return output[::-1]输出:
[3, 2, 1]
另:两种递归的代码
class TreeNode:def __init__(self, x):self.val = xself.left = Noneself.right = Nonedef PostOrder(t):'''直接打印'''if t != None:PostOrder(t.left)PostOrder(t.right)print(t.val, end = ' ')def PostOrderList(t):'''返回列表'''res = []if t != None:res.extend(PostOrderList(t.left))res.extend(PostOrderList(t.right))res.append(t.val)return resif __name__ == '__main__':t = TreeNode(1)t.right = TreeNode(2)t.right.left = TreeNode(3)PostOrder(t)print()print(PostOrderList(t))3. 接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:

输入:height = [0,1,0,2,1,0,1,3,2,1,2,1] 输出:6 解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5] 输出:9
提示:
n == height.length0 <= n <= 3 * 1040 <= height[i] <= 105
代码:
class Solution(object):def trap(self, height):ls = len(height)if ls == 0:return 0res, left = 0, 0while left < ls and height[left] == 0:left += 1pos = left + 1while pos < ls:if height[pos] >= height[left]:res += self.rain_water(height, left, pos)left = pospos += 1elif pos == ls - 1:max_value, max_index = 0, posfor index in range(left + 1, ls):if height[index] > max_value:max_value = height[index]max_index = indexres += self.rain_water(height, left, max_index)left = max_indexpos = left + 1else:pos += 1return resdef rain_water(self, height, start, end):if end - start <= 1:return 0min_m = min(height[start], height[end])res = min_m * (end - start - 1)step = 0for index in range(start + 1, end):if height[index] > 0:step += height[index]return res - stepif __name__ == '__main__':s = Solution()print (s.trap([2,6,3,8,2,7,2,5,0]))print (s.trap([0,1,0,2,1,0,1,3,2,1,2,1]))print (s.trap([4,2,0,3,2,5]))
输出:
11
6
9
附录
二叉树
二叉树(Binary Tree)是一种特殊的有序树型结构。
特点
(1)每个节点至多有两棵子树;
(2)二叉树的子树有左右之分;
(3)子树的次序不能任意颠倒(有序树)。
性质
(1)在二叉树的第i层上至多有2^(i-1)个节点(i>=1);
(2)深度为k的二叉树至多有2^k-1个节点(k>=1);
(3)对任何一棵二叉树,如果其叶子节点数为N0,度为2的结点数为N2,则N0=N2+1。
特殊二叉树
满二叉树
所有层的节点都达到最大数量,叶子除外的所有节点都有两个子节点,所有叶子都在最底一层(k)且数目为2^(k - 1)。即深度k且有2^k - 1个节点(叶子“长”满最后一层),或称完美二叉树 (Perfect Binary Tree)
完全二叉树
如果删除最底一层的所有叶子它就是满二叉树,即除了最后一层,每层节点都达到最大数量 ,即有深度k的个节点数在左闭右开【2^(k-1)+1,2^k-1】区间内。(Complete Binary Tree)
完全二叉树性质
1. 具有N个节点的完全二叉树的深度为[log2 N]+1,其中[x]为高斯函数,截尾取整。
2. 如果对一棵有n个节点的完全二叉树的节点按层序编号(从第一层到最后一层,每层从左到右),则对任一节点,有:
(1)如果i=1,则节点i是二叉树的根,无双亲;如果i>1,则其双亲节点为[i/2];
(2)如果2i>n,则节点i无左孩子;否则其左孩子是节点2i;
(3)如果2i+1>n,则节点i无右孩子;否则其右孩子是节点2i+1。
二叉树的遍历
指如何按某种搜索路径巡防树中的每个结点,使得每个结点均被访问一次,而且仅被访问一次。
常见的遍历方法有:先序、中序、后序遍历,一般都使用递归算法来实现。
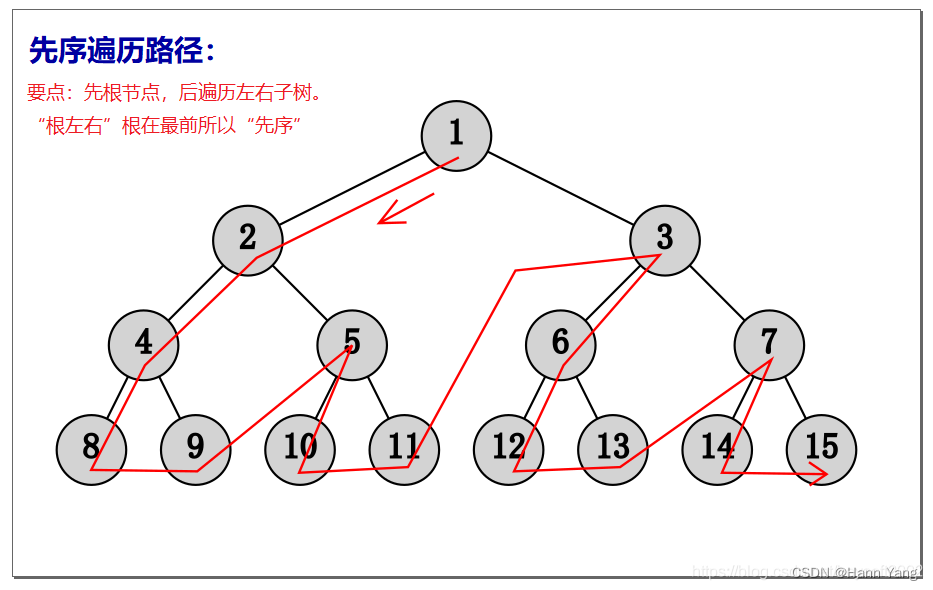
先序遍历
若二叉树为空,为空操作;
否则(1)访问根节点;(2)先序遍历左子树;(3)先序遍历右子树。
遍历结果: 1 [2 [4 8 9] [5 10 11]] [3 [6 12 13] [7 14 15] “根左右”
中序遍历
若二叉树为空,为空操作;
否则(1)中序遍历左子树;(2)访问根结点;(3)中序遍历右子树。
遍历结果: [[8 4 9] 2 [10 5 11]] 1 [[12 6 13] 3 [14 7 15]] “左根右”

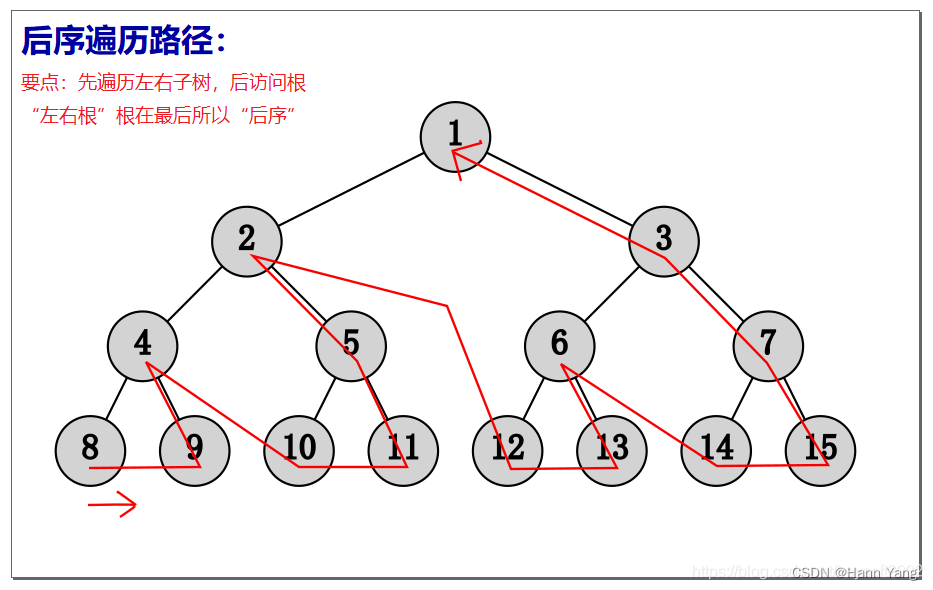
后序遍历
若二叉树为空,为空操作;
否则(1)后序遍历左子树;(2)后序遍历右子树;(3)访问根结点。
遍历结果: [[8 9 4] [10 11 5] 2] [[12 13 6] [14 15 7] 3] 1 “左右根”
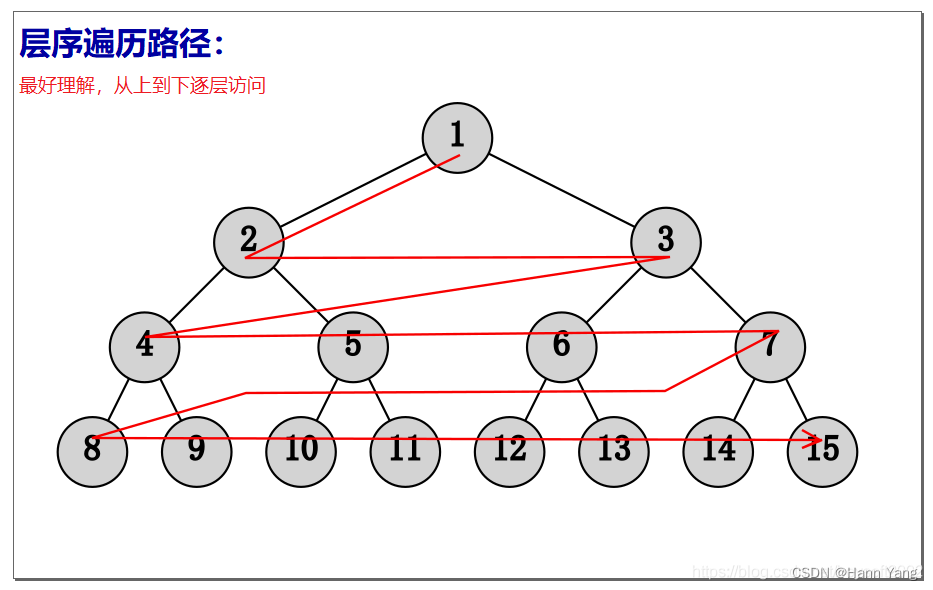
层序遍历
若二叉树为空,为空操作;否则从上到下、从左到右按层次进行访问。
遍历结果: 1 [2 3] [4 5 6 7] [8 9 10 11 12 13 14 15]
————————————————
End
