当前位置：首页 > news >正文

wordpress 排行榜网站主题广东今天新闻最新消息

news 2025/7/13 5:25:54

wordpress 排行榜网站主题,广东今天新闻最新消息,主题网络设计图幼儿园大班,个人做的网站有什么危险吗提示：DDU，供自己复习使用。欢迎大家前来讨论~ 文章目录二叉树 Part06二、题目题目一：669.修剪二叉搜索树解题思路：递归法迭代法： 题目二： 108.将有序数组转换为二叉搜索树解题思路递归法：迭代…

提示：DDU，供自己复习使用。欢迎大家前来讨论~

文章目录

二叉树 Part06
二、题目
题目一：669.修剪二叉搜索树
解题思路：
递归法
迭代法：

题目二： 108.将有序数组转换为二叉搜索树
解题思路
递归法：
迭代法

题目三：538.把二叉搜索树转换为累加树
解题思路：
递归法
迭代法

二叉树总结篇
二叉树的理论基础
二叉树的遍历方式
求二叉树的属性
二叉树的改造与修改
求二叉搜索树的属性
二叉树公共祖先问题
二叉搜索树的修改与改造

总结

二叉树 Part06

二、题目

题目一：669.修剪二叉搜索树

[669. 修剪二叉搜索树](https://leetcode.cn/problems/minimum-absolute-difference-in-bst/)

解题思路：

错误的思路：

直接想法就是：递归处理，然后遇到 root->val < low || root->val > high 的时候直接return NULL，一波修改，干净利落。

可以写出以下代码：

class Solution {
public:TreeNode* trimBST(TreeNode* root, int low, int high) {if (root == nullptr || root->val < low || root->val > high) return nullptr;root->left = trimBST(root->left, low, high);root->right = trimBST(root->right, low, high);return root;}
};

note：

但是会忽略掉删除节点的右子树，可能会存在符合的节点，但是上面的代码直接删除了，所以是不可行的。下图就是示例图：

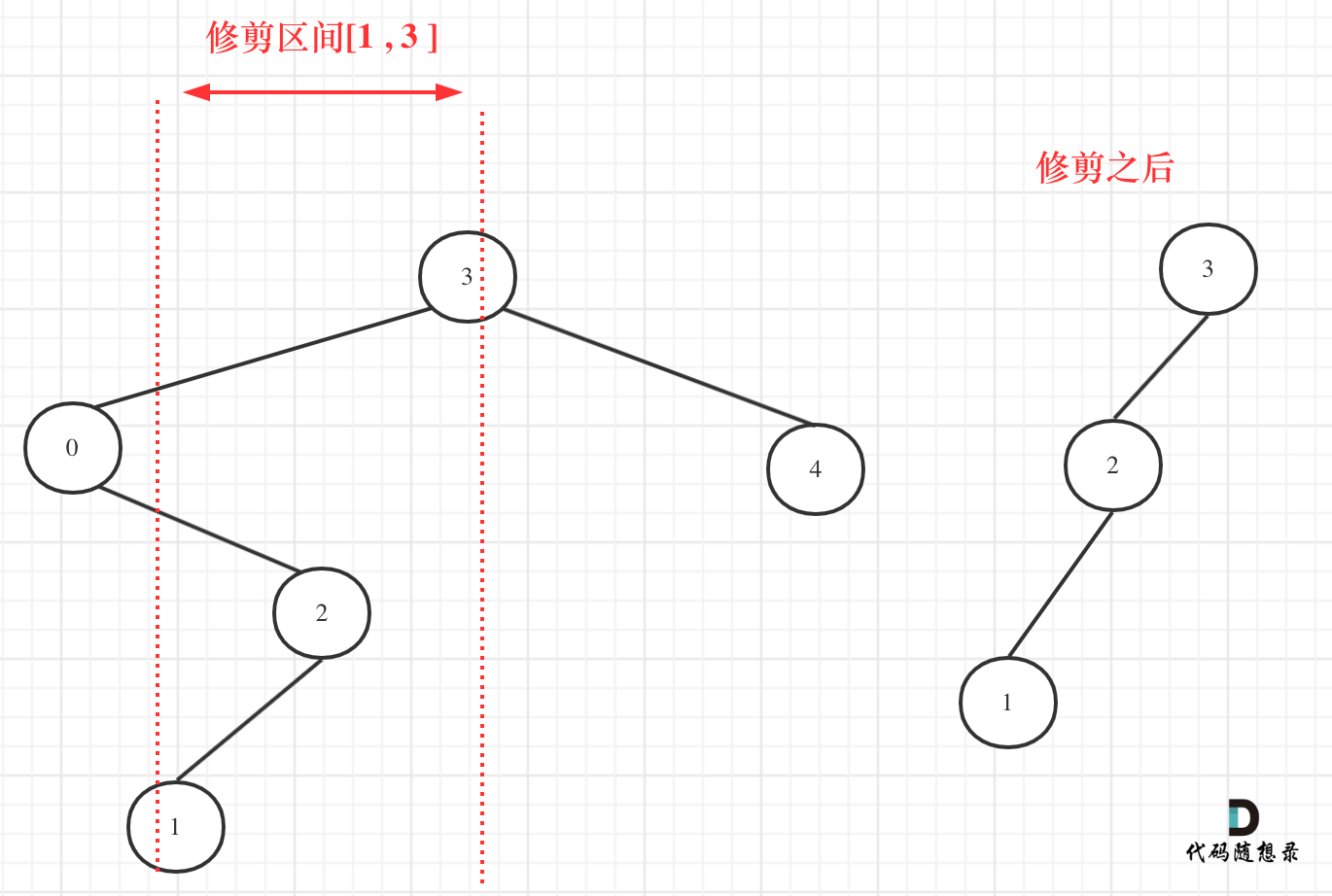
从图中可以看出需要重构二叉树，想想是不是本题就有点复杂了。

其实不用重构那么复杂。在上图中我们发现节点0并不符合区间要求，那么将节点0的右孩子节点2 直接赋给节点3的左孩子就可以了（就是把节点0从二叉树中移除），如图：

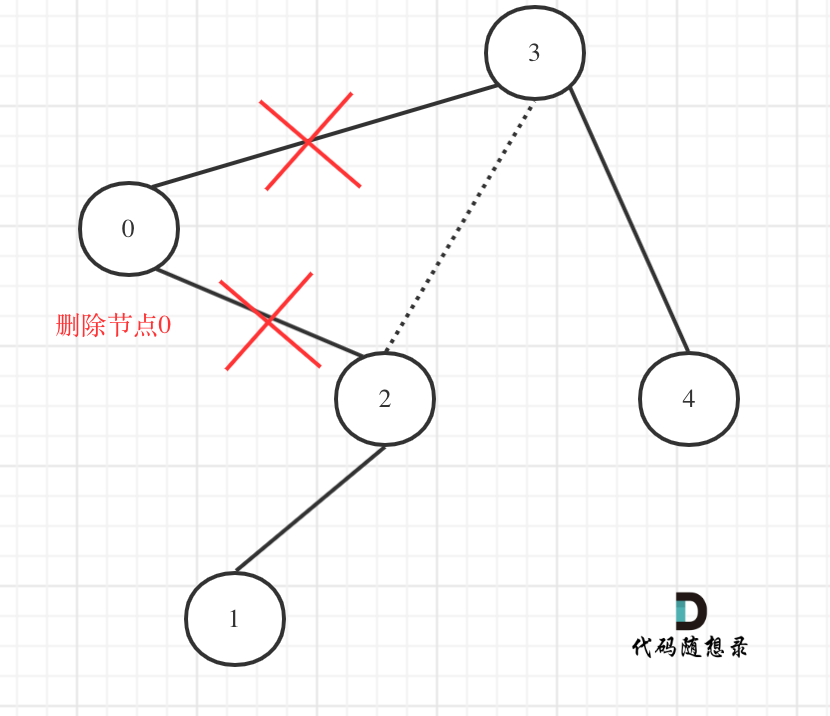
递归法

确定递归函数的参数以及返回值

这里我们为什么需要返回值呢？

因为是要遍历整棵树，做修改，其实不需要返回值也可以，我们也可以完成修剪（其实就是从二叉树中移除节点）的操作。

但是有返回值，更方便，可以通过递归函数的返回值来移除节点。
```
TreeNode* trimBST(TreeNode* root, int low, int high)
```
确定终止条件

修剪的操作并不是在终止条件上进行的，所以就是遇到空节点返回就可以了。
```
if (root == nullptr ) return nullptr;
```

确定单层递归的逻辑

如果root（当前节点）的元素小于low的数值，那么应该递归右子树，并返回右子树符合条件的头结点。

if (root->val < low) {TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点return right;
}// 同理如果root(当前节点)的元素大于high的，那么应该递归左子树，并返回左子树符合条件的头结点。
if (root->val > high) {TreeNode* left = trimBST(root->left, low, high); // 寻找符合区间[low, high]的节点return left;
}

接下来要将下一层处理完左子树的结果赋给root->left，处理完右子树的结果赋给root->right。

最后返回root节点，代码如下：

这里可能是子树里面还有不符合要求的节点，所以还是要遍历一下的。

root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子
root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子
return root;

Q：多余的节点究竟是如何从二叉树中移除的呢？

在回顾一下上面的代码，针对下图中二叉树的情况：

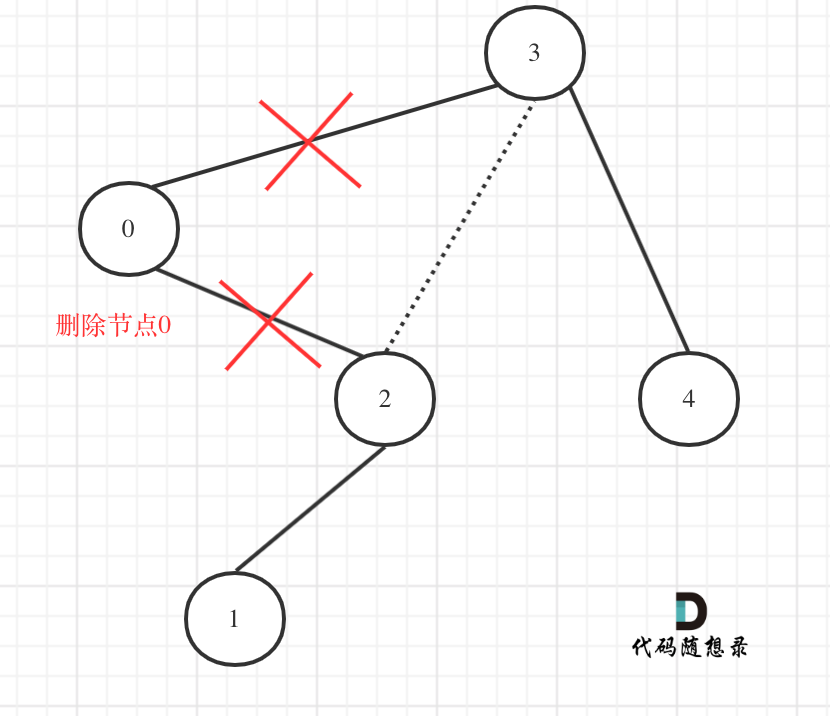
如下代码相当于把节点0的右孩子（节点2）返回给上一层，

if (root->val < low) {TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点return right;
}

然后如下代码相当于用节点3的左孩子把下一层返回的节点0的右孩子（节点2）接住。

root->left = trimBST(root->left, low, high);

此时节点3的左孩子就变成了节点2，将节点0从二叉树中移除了。

完整代码如下：

class Solution {
public:TreeNode* trimBST(TreeNode* root, int low, int high) {if (root == nullptr ) return nullptr;if (root->val < low) {TreeNode* right = trimBST(root->right, low, high); // 寻找符合区间[low, high]的节点return right;}if (root->val > high) {TreeNode* left = trimBST(root->left, low, high); // 寻找符合区间[low, high]的节点return left;}root->left = trimBST(root->left, low, high); // root->left接入符合条件的左孩子root->right = trimBST(root->right, low, high); // root->right接入符合条件的右孩子return root;}
};

精简之后：

class Solution {
public:TreeNode* trimBST(TreeNode* root, int low, int high) {if (root == nullptr) return nullptr;if (root->val < low) return trimBST(root->right, low, high);if (root->val > high) return trimBST(root->left, low, high);root->left = trimBST(root->left, low, high);root->right = trimBST(root->right, low, high);return root;}
};

迭代法：

因为二叉搜索树的有序性，不需要使用栈模拟递归的过程。

在剪枝的时候，可以分为三步：

将root移动到[L, R] 范围内，注意是左闭右闭区间
剪枝左子树
剪枝右子树

class Solution {
public:TreeNode* trimBST(TreeNode* root, int L, int R) {if (!root) return nullptr;// 处理头结点，让root移动到[L, R] 范围内，注意是左闭右闭while (root != nullptr && (root->val < L || root->val > R)) {if (root->val < L) root = root->right; // 小于L往右走else root = root->left; // 大于R往左走}TreeNode *cur = root;// 此时root已经在[L, R] 范围内，处理左孩子元素小于L的情况while (cur != nullptr) {while (cur->left && cur->left->val < L) {cur->left = cur->left->right;}cur = cur->left;}cur = root;// 此时root已经在[L, R] 范围内，处理右孩子大于R的情况while (cur != nullptr) {while (cur->right && cur->right->val > R) {cur->right = cur->right->left;}cur = cur->right;}return root;}
};

小结：

题目二： 108.将有序数组转换为二叉搜索树

108. 将有序数组转换为二叉搜索树

解题思路

本质就是寻找分割点，分割点作为当前节点，然后递归左区间和右区间。
因为有序数组构造二叉搜索树，寻找分割点就比较容易了。
分割点就是数组中间位置的节点。

Q：如果数组长度为偶数，中间节点有两个，取哪一个？

取哪一个都可以，只不过构成了不同的平衡二叉搜索树。

例如：输入：[-10,-3,0,5,9]

如下两棵树，都是这个数组的平衡二叉搜索树：

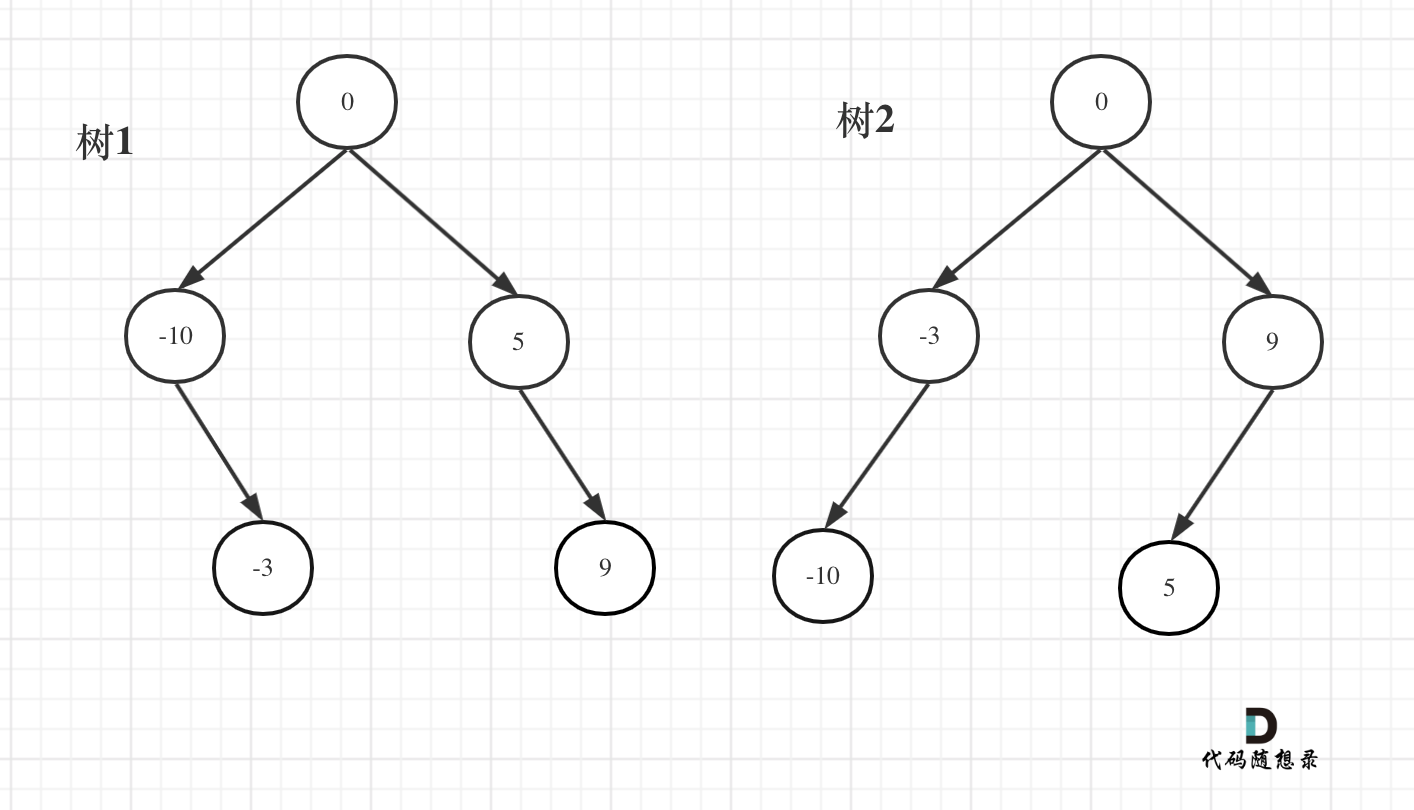
如果要分割的数组长度为偶数的时候，中间元素为两个，是取左边元素就是树1，取右边元素就是树2。

这也是题目中强调答案不是唯一的原因。

递归法：

确定递归函数的返回值及参数

这里定义的是左闭右闭区间，在不断分割的过程中，也会坚持左闭右闭的区间，这又涉及之前讲过的循环不变量。
```
// 左闭右闭区间[left, right]
TreeNode* traversal(vector<int>& nums, int left, int right)
```
确定递归终止条件

这里定义的是左闭右闭的区间，所以当区间 left > right的时候，就是空节点了。
```
if (left > right) return nullptr;
```
确定单层递归的逻辑

首先取数组中间元素的位置，不难写出int mid = (left + right) / 2;，这么写其实有一个问题，就是数值越界，例如left和right都是最大int，这么操作就越界了，在二分法中尤其需要注意！

**note：**所以可以这么写：int mid = left + ((right - left) / 2);

int mid = left + ((right - left) / 2);  //首先取数组中间元素的位置
TreeNode* root = new TreeNode(nums[mid]); //取了中间位置，就开始以中间位置的元素构造节点
root->left = traversal(nums, left, mid - 1); //接着划分区间，root的左孩子接住下一层左区间的构造节点，右孩子接住下一层右区间构造的节点。
root->right = traversal(nums, mid + 1, right);
return root;

这里int mid = left + ((right - left) / 2);的写法相当于是如果数组长度为偶数，中间位置有两个元素，取靠左边的。

整体C++代码如下：

class Solution {
private:TreeNode* traversal(vector<int>& nums, int left, int right) {if (left > right) return nullptr;int mid = left + ((right - left) / 2);TreeNode* root = new TreeNode(nums[mid]);root->left = traversal(nums, left, mid - 1);root->right = traversal(nums, mid + 1, right);return root;}
public:TreeNode* sortedArrayToBST(vector<int>& nums) {TreeNode* root = traversal(nums, 0, nums.size() - 1);return root;}
};

注意：在调用traversal的时候传入的left和right为什么是0和nums.size() - 1，因为定义的区间为左闭右闭。

迭代法

迭代法可以通过三个队列来模拟，一个队列放遍历的节点，一个队列放左区间下标，一个队列放右区间下标。

模拟的就是不断分割的过程，C++代码如下：

class Solution {
public:TreeNode* sortedArrayToBST(vector<int>& nums) {if (nums.size() == 0) return nullptr;TreeNode* root = new TreeNode(0);   // 初始根节点queue<TreeNode*> nodeQue;           // 放遍历的节点queue<int> leftQue;                 // 保存左区间下标queue<int> rightQue;                // 保存右区间下标nodeQue.push(root);                 // 根节点入队列leftQue.push(0);                    // 0为左区间下标初始位置rightQue.push(nums.size() - 1);     // nums.size() - 1为右区间下标初始位置while (!nodeQue.empty()) {TreeNode* curNode = nodeQue.front();nodeQue.pop();int left = leftQue.front(); leftQue.pop();int right = rightQue.front(); rightQue.pop();int mid = left + ((right - left) / 2);curNode->val = nums[mid];       // 将mid对应的元素给中间节点if (left <= mid - 1) {          // 处理左区间curNode->left = new TreeNode(0);nodeQue.push(curNode->left);leftQue.push(left);rightQue.push(mid - 1);}if (right >= mid + 1) {         // 处理右区间curNode->right = new TreeNode(0);nodeQue.push(curNode->right);leftQue.push(mid + 1);rightQue.push(right);}}return root;}
};

小结：

递归思路：提到了递归方法的核心思路是不断进行中间分割，然后递归地处理左区间和右区间，这也是一种分治策略。
递归函数的返回值：通过递归函数的返回值来增删二叉树是常规操作。
循环不变量的重要性：在定义区间的过程中，再次强调了循环不变量的重要性，这可能是在递归或迭代过程中保持逻辑一致性的关键。
迭代方法：这实际上是模拟取中间元素，然后不断分割去构造二叉树的过程。
递归与迭代的比较：虽然递归方法可能更直观，但迭代方法提供了另一种解决问题的途径，特别是在某些情况下可能更高效或更适合某些应用场景。

题目三：538.把二叉搜索树转换为累加树

538. 把二叉搜索树转换为累加树

解题思路：

当我们面对累加二叉搜索树的问题时，可能会感到困惑，因为直观上它看起来比操作数组要复杂。
使得每个节点 node 的新值等于原树中大于或等于 node.val 的值之和。
但一旦我们认识到二叉搜索树的有序性，问题就变得简单了。就像处理一个有序数组[2, 5, 13]，我们可以从后向前进行累加，得到新的数组[20, 18, 13]。
这种遍历方式在数组中很常见，而在二叉搜索树中，我们只需要调整遍历的顺序，采用反中序遍历（即先遍历右子树，然后是根节点，最后是左子树），就可以实现同样的顺序累加。这样一来，原本看似复杂的累加操作，就变成了一个简单的遍历和累加过程。

递归法

pre指针的使用技巧: 本题依然需要一个pre指针记录当前遍历节点cur的前一个节点，这样才方便做累加。

递归三部曲：

确定递归函数的返回值和参数

nt pre = 0; // 记录前一个节点的数值
void traversal(TreeNode* cur)

确定递归函数的终止条件
```
if (cur == NULL) return;
```
确定单层循环逻辑

注意要右中左来遍历二叉树，中节点的处理逻辑就是让cur的数值加上前一个节点的数值。
```
traversal(cur->right);  // 右
cur->val += pre;        // 中
pre = cur->val;
traversal(cur->left);   // 左
```

完整代码如下：

class Solution {
private:int pre = 0; // 记录前一个节点的数值void traversal(TreeNode* cur) { // 右中左遍历if (cur == NULL) return;traversal(cur->right);cur->val += pre;pre = cur->val;traversal(cur->left);}
public:TreeNode* convertBST(TreeNode* root) {pre = 0;traversal(root);return root;}
};

迭代法

迭代法其实就是中序模板题了,确定一个自己习惯的写法。

class Solution {
private:int pre; // 记录前一个节点的数值void traversal(TreeNode* root) {stack<TreeNode*> st;TreeNode* cur = root;while (cur != NULL || !st.empty()) {if (cur != NULL) {st.push(cur);cur = cur->right;   // 右} else {cur = st.top();     // 中st.pop();cur->val += pre;pre = cur->val;cur = cur->left;    // 左}}}
public:TreeNode* convertBST(TreeNode* root) {pre = 0;traversal(root);return root;}
};

二叉树总结篇

二叉树的理论基础

二叉树的种类、存储方式、遍历方式、定义方式

二叉树的遍历方式

深度优先遍历
广度优先遍历

求二叉树的属性

二叉树的改造与修改

求二叉搜索树的属性

二叉树公共祖先问题

二叉搜索树的修改与改造

小结：

note：二叉树的遍历顺序的选择

如果是要构造二叉树，无论是普通的二叉树还是二叉搜索树，通常都是先处理根节点，也就是前序遍历。
当我们想要计算普通二叉树的一些属性时，后序遍历是个不错的选择，因为这样可以在访问节点之前先得到其左右子树的信息，通常需要通过递归函数的返回值来进行计算。
而对于二叉搜索树，由于其元素是有序的，中序遍历是最佳选择，因为这样可以直接利用树的有序性，比如进行排序或查找操作。

注意在普通二叉树的属性中，用的是一般为后序，例如单纯求深度就用前序，二叉树：找所有路径 (opens new window)也用了前序，这是为了方便让父节点指向子节点。

所以求普通二叉树的属性还是要具体问题具体分析，才能让问题变得简洁。

总结

学到了那些东西:

二叉树的构造（前序构造），二叉树的遍历方式（前中后）
递归和迭代，一般递归的思路来的比较简单，代码也是比较简洁。递归三部曲（1.2.3）。
pre指针的使用，这是一个技巧。
看到二叉搜索树，一定要记得利用他的特性，有序。（在本节，迭代的代码也是比较简单的。）

关于二叉树的章节，今天是完结篇，整体下来，学的有些稀里糊涂，大概过了一边，顺了一遍思路。很多题目自己为了节省时间，还有偷懒，就没有自己亲手去敲的，不知道是因为自己太懒还是太烂，总有畏难情绪，觉得自己敲了也敲不对，敲了也没用只是浪费时间，就有些投机取巧，没有去敲。这样下来，总感觉收获很少，但哪位老板能和我说一下，你们是怎么坚持，每题都敲代码的吗？（这对我很重要）

总之，二叉树，这一个章节也是结束了，马上要开始一个新的章节回溯，杜绝懒惰，从我做起，加油！！

查看全文

http://www.khdw.cn/news/31171.html