本地服务器怎么做网站seo外包公司哪家专业
归并排序是一种遵循分而治之方法的排序算法。它的工作原理是递归地将输入数组划分为较小的子数组并对这些子数组进行排序,然后将它们合并在一起以获得排序后的数组。
简单来说,归并排序的过程就是将数组分成两半,对每一半进行排序,然后将已排序的两半合并在一起。重复这个过程,直到整个数组排序完毕。

归并排序算法
归并排序是如何工作的?
归并排序是一种流行的排序算法,以其高效和稳定而闻名。它遵循分而治之的方法对给定的元素数组进行排序。
以下是合并排序如何工作的分步说明:
1、划分:递归地将列表或数组划分为两半,直到不能再划分为止。
2、征服:使用合并排序算法对每个子数组进行单独排序。
3、合并:已排序的子数组按排序顺序合并在一起。该过程将继续,直到两个子数组中的所有元素都已合并。
归并排序示意图:
让我们使用归并排序对数组或列表[38, 27, 43, 10]进行排序
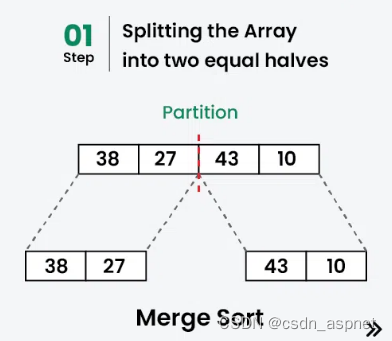

让我们看看上面例子的工作原理:
划分:
[38, 27, 43, 10]分为[38, 27 ] 和[43, 10]。
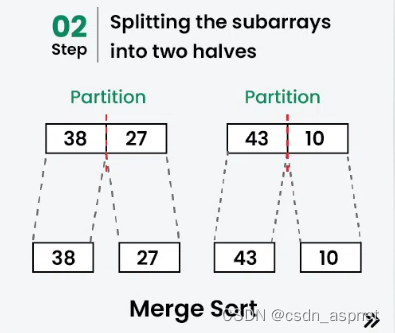
[38, 27]分为[38]和[27]。
[43, 10]分为[43]和[10]。
征服:
[38]已经排序。
[27]已经排序。
[43]已经排序。
[10]已经排序。
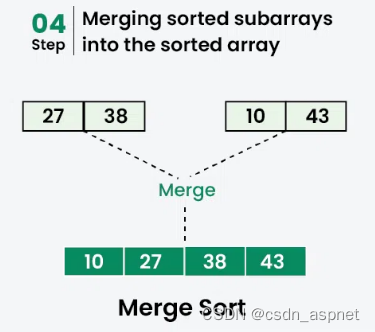
合并:
合并[38]和[27]得到[27, 38]。
合并[43]和[10]得到[10,43]。
合并[27, 38]和[10,43]得到最终的排序列表[10, 27, 38, 43]
因此,排序列表为[10, 27, 38, 43]。
归并排序的实现:
// C++ program for Merge Sort
#include <bits/stdc++.h>
using namespace std;
// Merges two subarrays of array[].
// First subarray is arr[begin..mid]
// Second subarray is arr[mid+1..end]
void merge(int array[], int const left, int const mid,
int const right)
{
int const subArrayOne = mid - left + 1;
int const subArrayTwo = right - mid;
// Create temp arrays
auto *leftArray = new int[subArrayOne],
*rightArray = new int[subArrayTwo];
// Copy data to temp arrays leftArray[] and rightArray[]
for (auto i = 0; i < subArrayOne; i++)
leftArray[i] = array[left + i];
for (auto j = 0; j < subArrayTwo; j++)
rightArray[j] = array[mid + 1 + j];
auto indexOfSubArrayOne = 0, indexOfSubArrayTwo = 0;
int indexOfMergedArray = left;
// Merge the temp arrays back into array[left..right]
while (indexOfSubArrayOne < subArrayOne
&& indexOfSubArrayTwo < subArrayTwo) {
if (leftArray[indexOfSubArrayOne]
<= rightArray[indexOfSubArrayTwo]) {
array[indexOfMergedArray]
= leftArray[indexOfSubArrayOne];
indexOfSubArrayOne++;
}
else {
array[indexOfMergedArray]
= rightArray[indexOfSubArrayTwo];
indexOfSubArrayTwo++;
}
indexOfMergedArray++;
}
// Copy the remaining elements of
// left[], if there are any
while (indexOfSubArrayOne < subArrayOne) {
array[indexOfMergedArray]
= leftArray[indexOfSubArrayOne];
indexOfSubArrayOne++;
indexOfMergedArray++;
}
// Copy the remaining elements of
// right[], if there are any
while (indexOfSubArrayTwo < subArrayTwo) {
array[indexOfMergedArray]
= rightArray[indexOfSubArrayTwo];
indexOfSubArrayTwo++;
indexOfMergedArray++;
}
delete[] leftArray;
delete[] rightArray;
}
// begin is for left index and end is right index
// of the sub-array of arr to be sorted
void mergeSort(int array[], int const begin, int const end)
{
if (begin >= end)
return;
int mid = begin + (end - begin) / 2;
mergeSort(array, begin, mid);
mergeSort(array, mid + 1, end);
merge(array, begin, mid, end);
}
// UTILITY FUNCTIONS
// Function to print an array
void printArray(int A[], int size)
{
for (int i = 0; i < size; i++)
cout << A[i] << " ";
cout << endl;
}
// Driver code
int main()
{
int arr[] = { 12, 11, 13, 5, 6, 7 };
int arr_size = sizeof(arr) / sizeof(arr[0]);
cout << "Given array is \n";
printArray(arr, arr_size);
mergeSort(arr, 0, arr_size - 1);
cout << "\nSorted array is \n";
printArray(arr, arr_size);
return 0;
}
// This code is contributed by Mayank Tyagi
// This code was revised by Joshua Estes
输出
给定数组是
12 11 13 5 6 7
排序后的数组是
5 6 7 11 12 13
归并排序的复杂度分析:
时间复杂度:
最佳情况: O(n log n),当数组已经排序或接近排序时。
平均情况: O(n log n),当数组随机排序时。
最坏情况: O(n log n),当数组按相反顺序排序时。
空间复杂度: O(n),合并时使用的临时数组需要额外的空间。
归并排序的优点:
稳定性:归并排序是一种稳定的排序算法,这意味着它保持输入数组中相等元素的相对顺序。
保证最坏情况下的性能:归并排序的最坏情况时间复杂度为O(N logN),这意味着即使在大型数据集上它也能表现良好。
易于实现:分而治之的方法很简单。
归并排序的缺点:
空间复杂度:归并排序在排序过程中需要额外的内存来存储合并后的子数组。
非就地:合并排序不是就地排序算法,这意味着它需要额外的内存来存储排序后的数据。这对于关注内存使用的应用程序来说可能是一个缺点。
归并排序的应用:
对大型数据集进行排序
外部排序(当数据集太大而无法容纳在内存中时)
反转计数(计算数组中反转的次数)
查找数组的中位数
