全国疫苗接种率最新数据云seo关键词排名优化软件
一.LCA介绍
![]()
LCA通常指的是“最近共同祖先”(Lowest Common Ancestor)。LCA是一种用于解决树或图结构中两个节点的最低共同祖先的问题的算法。
在树结构中,LCA是指两个节点的最近层级的共同祖先节点。例如,考虑一棵树,其中节点A是节点B和节点C的祖先,而节点D是节点B和节点C的共同祖先,但节点D不是最低层级的共同祖先。在这种情况下,LCA就是节点D。
LCA算法在计算机科学中有广泛的应用,例如在计算树的最近公共祖先、解决图的连通性问题、计算有向无环图(DAG)的最近公共祖先等方面。常见的LCA算法包括基于深度优先搜索(DFS)的算法、基于倍增法的算法和Tarjan算法等。
LCA算法的实现方式取决于所使用的数据结构和具体问题的要求。它可以通过预处理树结构,计算和存储每个节点的深度或其他相关信息,以加快查询的速度。LCA算法的时间复杂度通常为O(logN)或O(1),其中N是树或图中的节点数量。
总之,LCA算法是解决树或图结构中两个节点最低共同祖先的问题的一种常见算法。
二.倍增法求LCA
![]()
倍增法(Binary Lifting)是一种常用的求解最低共同祖先(LCA)问题的算法。它通过预处理和存储每个节点的跳跃祖先,以实现快速查询LCA的目的。下面是倍增法求解LCA的详细步骤:
-
预处理:对于每个节点v,计算并存储它的第2^i个祖先,其中i从0开始逐渐增加。这可以通过深度优先搜索(DFS)遍历树来完成。对于根节点,其第2^i个祖先就是根节点本身。对于其他节点v,其第2^i个祖先可以通过它的第2^(i-1)个祖先的第2^(i-1)个祖先来计算。
-
查询LCA:给定两个节点u和v,首先比较它们的深度,假设u的深度大于v的深度。然后,通过不断向上跳跃u的祖先,使得u和v的深度相等。具体步骤如下:
- 如果u和v的深度不相等,将u向上跳跃到与v深度相等的位置。这可以通过从最高位开始逐渐减小的方式进行,即从最大的i开始,如果u的第2^i个祖先的深度大于等于v的深度,则将u跳跃到第2^i个祖先。
- 然后,同时向上跳跃u和v,直到它们的第一个公共祖先出现。这可以通过从最高位开始逐渐减小的方式进行,即从最大的i开始,如果u的第2^i个祖先和v的第2^i个祖先不相等,则将u和v同时跳跃到它们的第2^i个祖先。
- 最后,u和v的第一个公共祖先就是LCA。
倍增法求解LCA的时间复杂度为O(logN),其中N是树中的节点数量。这是因为在查询LCA时,每次跳跃都会将节点的深度减半,直到找到LCA为止。
总结起来,倍增法是一种通过预处理和存储节点的跳跃祖先来求解LCA问题的算法。它具有较低的时间复杂度,并且适用于静态树结构,即树结构不会发生变化的情况下。
三.题目
P3379 【模板】最近公共祖先(LCA) - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)
四.代码
#include<bits/stdc++.h>
#define maxn 500005
using namespace std;
int n,m,s; //点,次数,根节点
//链式前向星
int cnt=0,head[maxn];
struct Edge{int u,v,next;
}edge[maxn<<1];
void add(int u,int v){edge[++cnt]=(Edge){u,v,head[u]};head[u]=cnt;
}
//建树
int depth[maxn],p[maxn][25];
void dfs(int u,int fa){p[u][0]=fa;depth[u]=depth[fa]+1;for(int i=head[u];i;i=edge[i].next){int v=edge[i].v;if(v==fa) continue; //防止套娃,无线循环dfs(v,u); }
}
int lca(int x,int y){if(depth[x]<depth[y]) swap(x,y);for(int j=24;j>=0;j--){if(depth[x]-(1<<j)>=depth[y]){x=p[x][j]; //往上走 }}//特判&&巧合if(x==y) return x;//现在x和y深度差不多,同时上升for(int j=24;j>=0;j--){if(p[x][j]!=p[y][j]){x=p[x][j]; y=p[y][j];}} return p[x][0];
}
int main(){cin>>n>>m>>s;for(int i=1;i<n;i++){int u,v;cin>>u>>v;add(u,v);add(v,u);}dfs(s,0); //建树 //预处理 for(int j=1;(1<<j)<=n;j++){ //长度 2^j<=n for(int i=1;i<=n;i++){p[i][j]=p[p[i][j-1]][j-1];}} //输出答案&&LCAwhile(m--){int x,y;cin>>x>>y;cout<<lca(x,y)<<endl;} return 0;
}五.卡住笔者的一个小问题
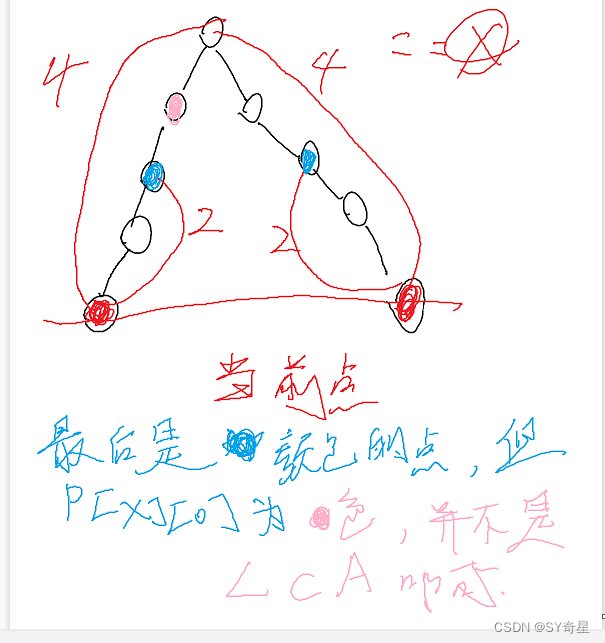
六.answer:
注意: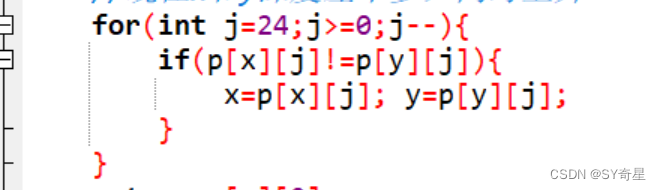
找到p[x][j]!=p[y][j]的时候,并没有直接break;
而是赋值后继续,也就是意味着(结合我的疑问)j再=0,再往上跳1步才结束
这时就成功到达pick点,最后return p[x][0]即为LCA;
其实就妙在遍历中找到!=时,赋值后继续遍历,这就解决了LCA不在倍增数的情况!
