湖北网站建设价格b2b采购平台
电子技术——BJT差分输入对

本节我们来讨论BJT差分输入对。
共模输入
下图是BJT差分输入对的基本原理图:
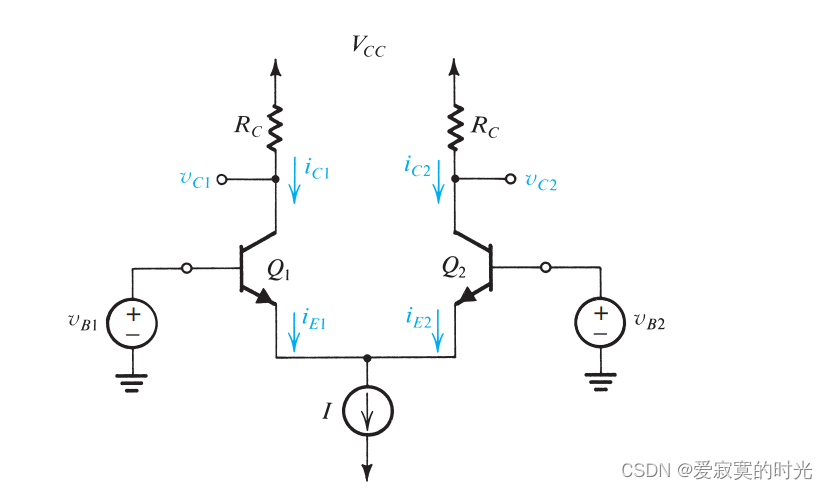
首先我们考虑两端输入共模信号 VCMV_{CM}VCM :
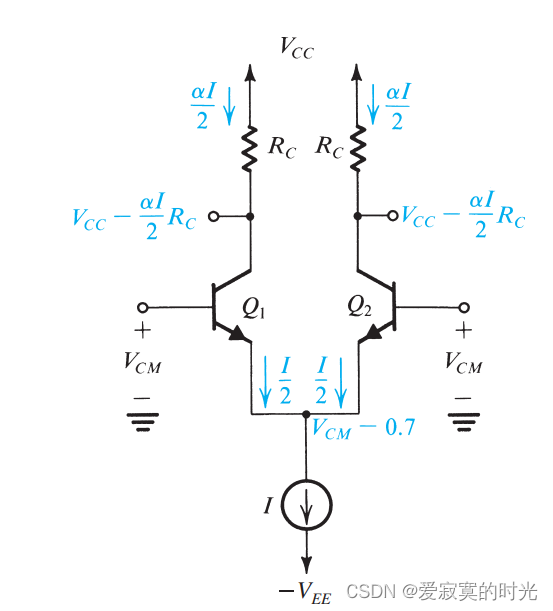
此时 vB1=vB2=VCMv_{B1} = v_{B2} = V_{CM}vB1=vB2=VCM 因为电路的对称结构,所以 iE1=iE2=I/2i_{E1} = i_{E2} = I/2iE1=iE2=I/2 ,发射极电压为 VCM−VBEV_{CM} - V_{BE}VCM−VBE 这里 VBEV_{BE}VBE 是满足电流 iE1=iE2=I/2i_{E1} = i_{E2} = I/2iE1=iE2=I/2 的基极电压(大约在0.7V)。输出的集电极电压为:
vo=VCC−αI2RCv_o = V_{CC} - \frac{\alpha I}{2}R_C vo=VCC−2αIRC
输出端两端电压相同,差值为零。这说明BJT差分输入对同样对共模信号无响应。
对于BJT差分输入对的共模信号输入范围,存在上限,当 Q1Q_1Q1 和 Q2Q_2Q2 处于饱和区边界的时候,此时:
VCMmax≃VC+0.4=VCC−αI2RC+0.4V_{CMmax} \simeq V_C + 0.4 = V_{CC} - \frac{\alpha I}{2}R_C + 0.4 VCMmax≃VC+0.4=VCC−2αIRC+0.4
存在下限,使得电流源 III 有最小的压降 VCSV_{CS}VCS :
VCMmin=−VEE+VCS+VBEV_{CMmin} = -V_{EE} + V_{CS} + V_{BE} VCMmin=−VEE+VCS+VBE
大信号模型
根据BJT的电压电流传导关系,我们知道:
iE1=ISαevB1−vE/VTi_{E1} = \frac{I_S}{\alpha} e^{v_{B1} - v_{E}/V_T} iE1=αISevB1−vE/VT
iE2=ISαevB2−vE/VTi_{E2} = \frac{I_S}{\alpha} e^{v_{B2} - v_{E}/V_T} iE2=αISevB2−vE/VT
做除法得到:
iE1iE2=e(vB1−vB2)/VT\frac{i_{E1}}{i_{E2}} = e^{(v_{B1} - v_{B2})/V_T} iE2iE1=e(vB1−vB2)/VT
以及我们有 iE1+iE2=Ii_{E1} + i_{E2} = IiE1+iE2=I ,解得:
iE1=I1+e−vid/VTi_{E1} = \frac{I}{1 + e^{-v_{id}/V_T}} iE1=1+e−vid/VTI
iE2=I1+evid/VTi_{E2} = \frac{I}{1 + e^{v_{id}/V_T}} iE2=1+evid/VTI
这里 vid=vB1−vB2v_{id} = v_{B1} - v_{B2}vid=vB1−vB2 ,集电极电流等于发射极电流的 α\alphaα 倍,非常接近单位一。
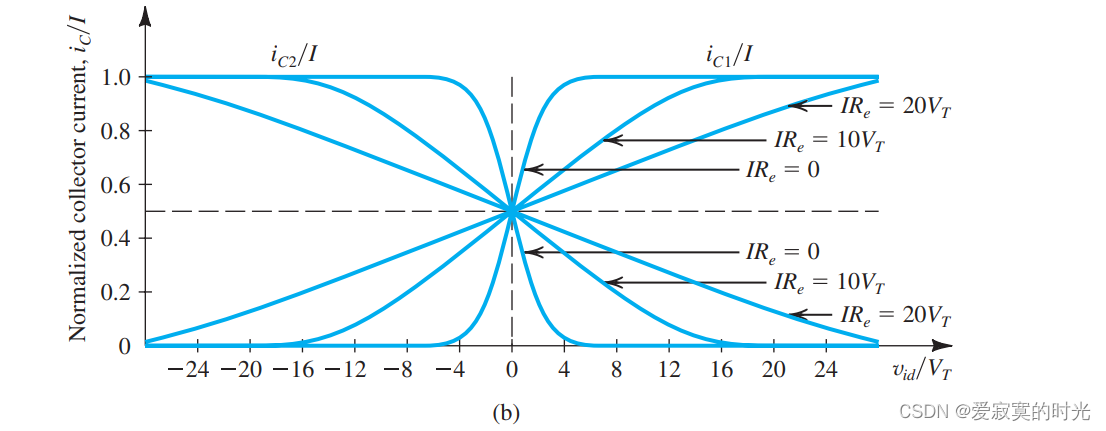
下图展示了归一化之后的差分响应的图形表示:
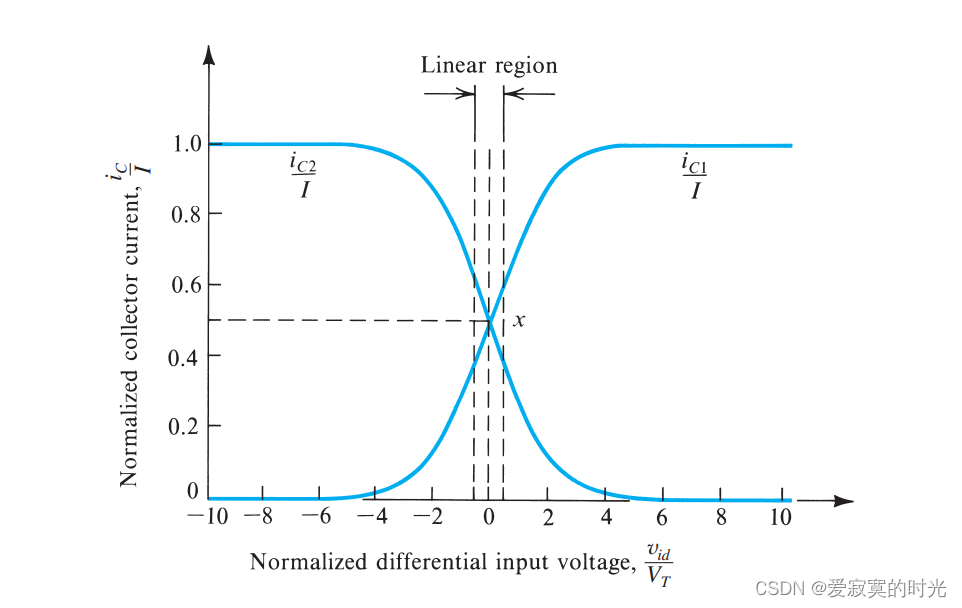
我们发现,当 vid=4VTv_{id} = 4V_Tvid=4VT (100mV)的时候,就会出现一个BJT截止另一个BJT完全导通的的情况,这比MOS的边界 2VOV\sqrt{2}V_{OV}2VOV 要小。实际上,BJT具有从一边切换到另一边更快的速度。
若获得较好的线性区域,必须让输入的差分信号小于 VT/2V_T/2VT/2 。最后,我们介绍一种扩宽BJT线性区域的方法,我们使用发射极电阻,如图所示:
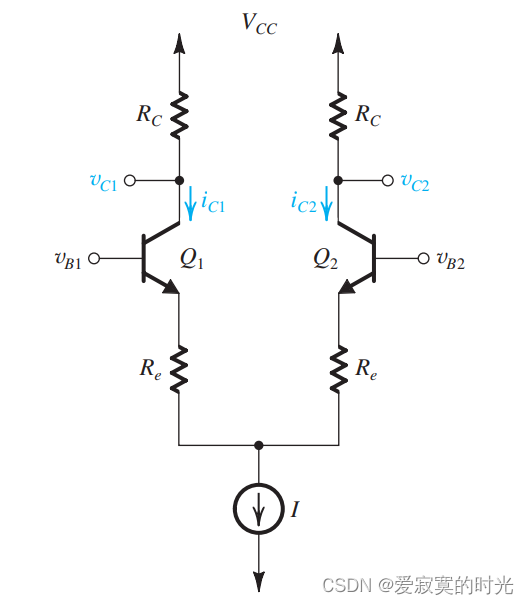
我们之前在BJT章节学习过,引入BJT的发射极电阻之后,由于发射极电阻的分压作用,可以扩大我们信号的幅值范围,进而扩宽BJT线性区域,结果可以参考下图:
但是代价是降低了增益系数。这种方法对于MOS差分输入对同样有效。
小信号模型
下图展示了我们小信号模型的原始电路图:
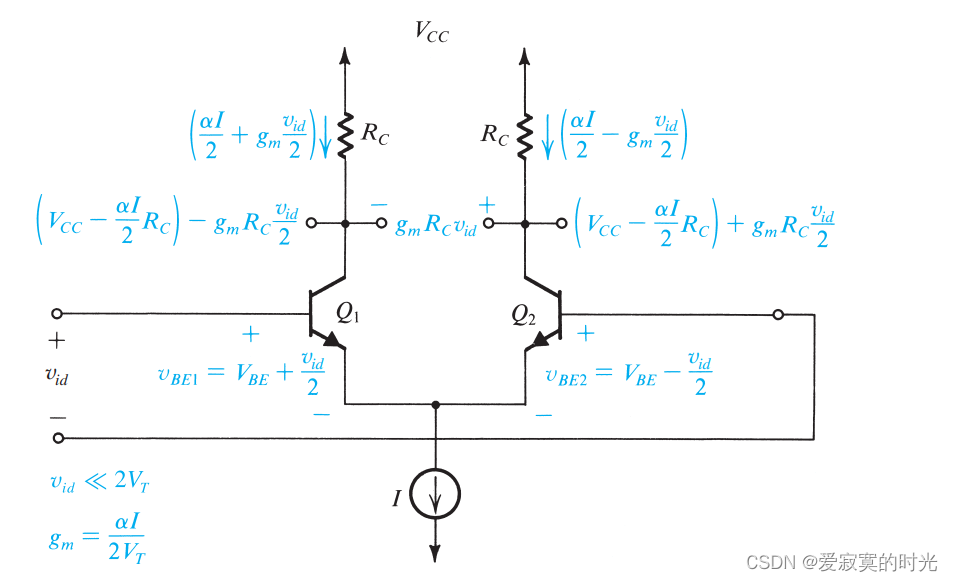
差分信号输入 vidv_{id}vid 通过互补输入到BJT差分输入对。此时集电极的信号电流为:
ic1=αI1+e−vid/VTi_{c1} = \frac{\alpha I}{1 + e^{-v_{id}/V_T}} ic1=1+e−vid/VTαI
ic2=αI1+evid/VTi_{c2} = \frac{\alpha I}{1 + e^{v_{id}/V_T}} ic2=1+evid/VTαI
将 ic1i_{c1}ic1 的分子分母同时乘以 evid/2VTe^{v_{id}/2V_T}evid/2VT :
ic1=αIevid/2VTevid/2VT+e−vid2/VTi_{c1} = \frac{\alpha I e^{v_{id}/2V_T}}{e^{v_{id}/2V_T} + e^{-v_{id}2/V_T}} ic1=evid/2VT+e−vid2/VTαIevid/2VT
假设 vid≪2VTv_{id} \ll 2V_Tvid≪2VT ,我们 exe^xex 展开只保留前两项:
ic1≃αI(1+vid/2VT)1+vid/2VT+1−vid/2VT=αI2+αI2VTvid2i_{c1} \simeq \frac{\alpha I(1+v_{id}/2V_T)}{1+v_{id}/2V_T + 1-v_{id}/2V_T} = \frac{\alpha I}{2} + \frac{\alpha I}{2V_T}\frac{v_{id}}{2} ic1≃1+vid/2VT+1−vid/2VTαI(1+vid/2VT)=2αI+2VTαI2vid
同理:
ic1≃αI2−αI2VTvid2i_{c1} \simeq \frac{\alpha I}{2} - \frac{\alpha I}{2V_T}\frac{v_{id}}{2} ic1≃2αI−2VTαI2vid
所以BJT差分输入对的差分电流为:
ic=αI2VTvid2i_c = \frac{\alpha I}{2V_T}\frac{v_{id}}{2} ic=2VTαI2vid
这表明,当应用差分信号输入 vidv_{id}vid 的时候, ic1i_{c1}ic1 会增加 ici_cic 而 ic2i_{c2}ic2 会降低 ici_cic 但保持总量不变一直为 III 。
另外一种解释为,BJT的互导系数为:
gm=ICVT=αI/2VTg_m = \frac{I_C}{V_T} = \frac{\alpha I/2}{V_T} gm=VTIC=VTαI/2
对于每一个BJT的输入信号电压都是 vid2\frac{v_{id}}{2}2vid ,故写作是:
ic=gmvid2i_c = g_m \frac{v_{id}}{2} ic=gm2vid
同样我们可以使用T模型解释:
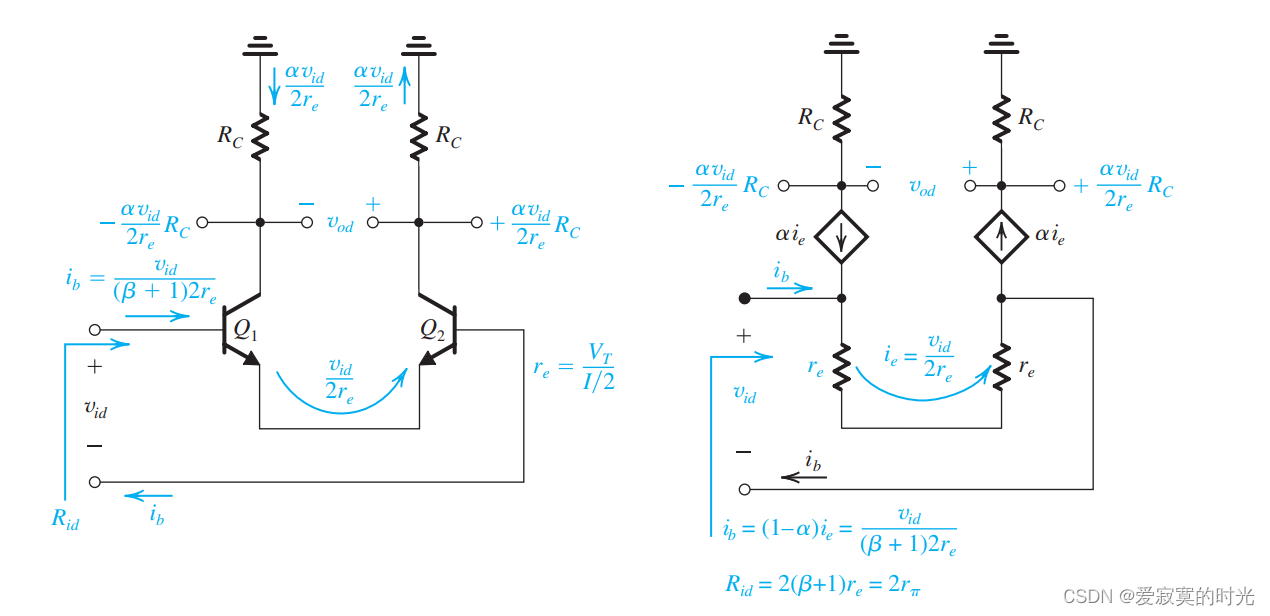
根据基尔霍夫定律,电压 vidv_{id}vid 作用在 2re2r_e2re 的总电阻中,此时:
ie=vid2rei_e = \frac{v_{id}}{2 r_e} ie=2revid
则此时的集电极电流为:
ic=αvid2re=gmvid2i_c = \alpha \frac{v_{id}}{2 r_e} = g_m \frac{v_{id}}{2} ic=α2revid=gm2vid
同样的分析方法适用于分析带发射极电阻的情况,如图:
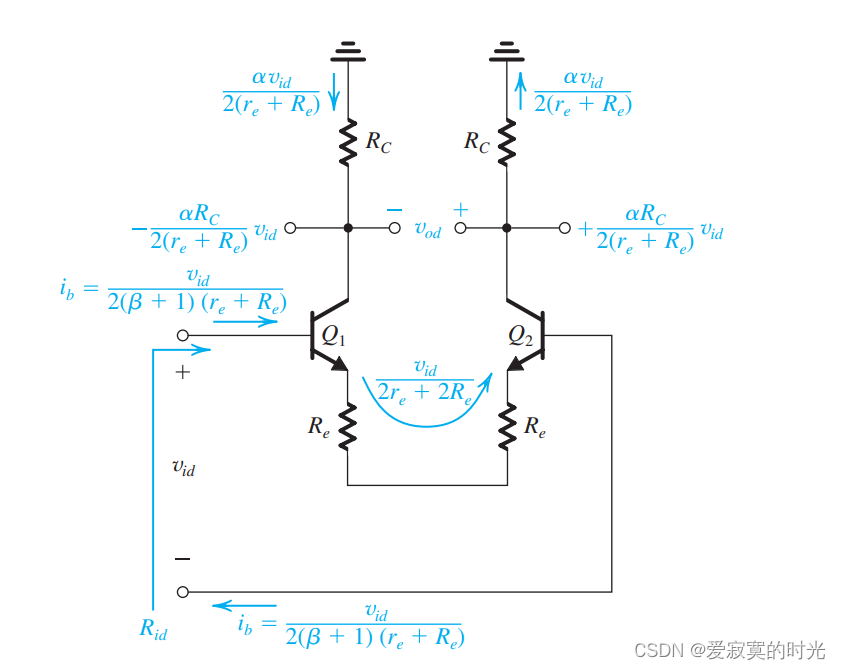
此时:
ie=vid2re+2Rei_e = \frac{v_{id}}{2r_e + 2R_e} ie=2re+2Revid
BJT不像MOS存在无穷大阻抗,现在让我们来计算BJT差分输入对的输入阻抗,我们知道两个输入端的基极电流相等,且都为:
ib=ieβ+1=vid/2reβ+1i_b = \frac{i_e}{\beta + 1} = \frac{v_{id}/2r_e}{\beta + 1} ib=β+1ie=β+1vid/2re
因此输入阻抗为:
Rid≡vidib=(β+1)2re=2rπR_{id} \equiv \frac{v_{id}}{i_b} = (\beta + 1)2r_e = 2r_\pi Rid≡ibvid=(β+1)2re=2rπ
这同样遵循电阻反射定律,即从两个基极看过去的电阻等于发射极电阻的 β+1\beta + 1β+1 倍。所以带发射极电阻的输入阻抗为:
Rid=2(β+1)(re+Re)R_{id} = 2(\beta + 1)(r_e + R_e) Rid=2(β+1)(re+Re)
接下来考虑电压增益,我们知道输出端的电压为:
vC1=(VCC−ICRC)−gmRCvid2v_{C1} = (V_{CC} - I_CR_C) - g_mR_C\frac{v_{id}}{2} vC1=(VCC−ICRC)−gmRC2vid
vC2=(VCC−ICRC)+gmRCvid2v_{C2} = (V_{CC} - I_CR_C) + g_mR_C\frac{v_{id}}{2} vC2=(VCC−ICRC)+gmRC2vid
这里 gmg_mgm 是BJT偏置在电流为 ICI_CIC 处的互导系数,且 ICI_CIC 为:
IC=αI2I_C = \frac{\alpha I}{2} IC=2αI
当使用差分输出的时候,此时电压增益为:
Ad=vodvid=gmRCA_d = \frac{v_{od}}{v_{id}} = g_mR_C Ad=vidvod=gmRC
当使用发射极电阻的时候,电压增益为:
Ad=α(2RC)2re+2Re≃RCre+ReA_d = \frac{\alpha (2R_C)}{2r_e + 2R_e} \simeq \frac{R_C}{r_e + R_e} Ad=2re+2Reα(2RC)≃re+ReRC
这同样满足电压增益为集电极总电阻比上发射极总电阻。
下图展示了一个不同的BJT差分输入对:
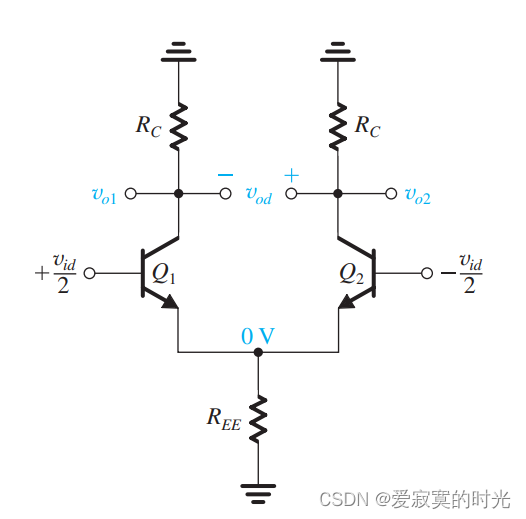
图中我们使用的互补输入方式,而且我们使用共发射极电阻 REER_{EE}REE 来代替偏置的恒流源,因为电路总是对称的,所以共发射极节点处的电压总是是为零,因此上面的电路等效于下面的半电路:
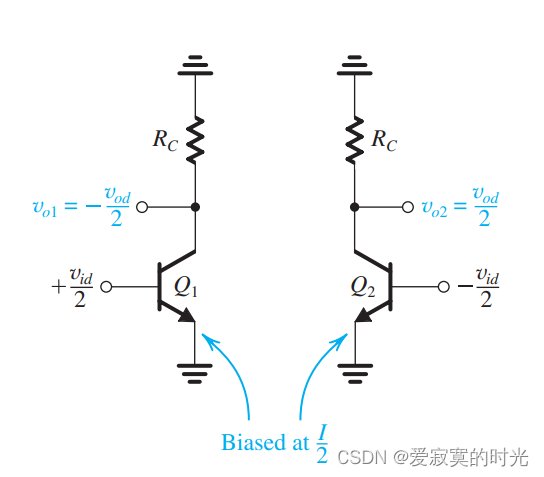
虽然 REER_{EE}REE 的阻抗是有限的,但是这并不影响信号分析中,BJT的发射极永远是虚拟AC地,因此 REER_{EE}REE 的有限阻抗不影响BJT差分输入对。
有时候,并不总是使用互补输入方式,另一种可能的输入方式是一端接地,一端输入,如图:
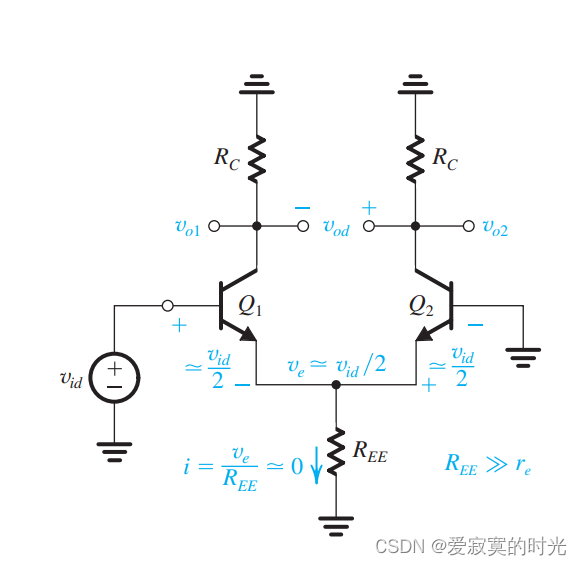
此时发射极电压不再是零,电阻 REER_{EE}REE 对信号存在影响。若假设 REE≫reR_{EE} \gg r_eREE≫re 则可以近似的看成是 ve=vid/2v_e = v_{id} / 2ve=vid/2 ,此时整个电路等价于互补输入方式,半电路分析仍可以使用,如上图。
互补输入方式中,两个半电路完全一致,因此只需要分析电路的一半即可,这种方法称为 差分半电路 。我们将其中一个半电路使用混合 π\piπ 模型:
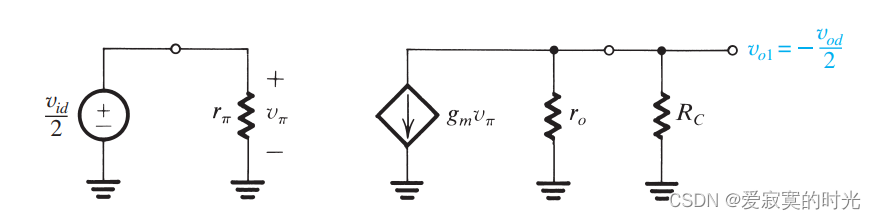
分析方法和我们之前分析共发射极电路分析方法一致,此时偏置电流为 I/2I/2I/2 。若考虑 ror_oro 的影响,我们有:
Ad=gm(RC∣∣ro)A_d = g_m(R_C || r_o) Ad=gm(RC∣∣ro)
BJT差分输入对的输入阻抗是半电路输入阻抗的两倍。
