制作网页的过程中可以单击什么标签显示网页效果seoul怎么读

目录
一、字符串转换问题
1.1问题
1.2确定动态规则(DP、状态转移方程)、初始值
(1)插入操作实现状态转移
(2)删除操作实现状态转移
(3)替换操作实现状态转移
(4)初始值
1.3动态规划算法代码实现
(1)完整代码
(2)程序速度优化
二、矩阵变换问题
2.1问题
2.2矩阵乘法
(1)矩阵相乘的条件
(2)矩阵乘法原理
(3)矩阵乘法符合结合律
(4)两个矩阵相乘的乘法运算个数（次数）
(5)结合律下的多个矩阵相乘的乘法运算个数（次数）
(6)多个矩阵连乘所得矩阵的行、列数
2.3确定动态规则(DP、状态转移方程)
1、子状态空间与子状态
2、动态规则(DP、状态转移方程)
2.4确定初始值
2.5状态转移的因素
2.6动态规划算法代码实现

动态规划算法实现------转换(编辑、变换)问题

一、字符串转换问题

1.1问题

       编辑距离(Edit Distance)，又叫Levenshtein距离(Levenshtein Distance)，对于两个字符串(或单词)，把一个字符串转换成另一个字符串所需的最少操作次数。

1.2确定动态规则(DP、状态转移方程)、初始值

       记A=’kitten’，B=’ sitting’，求A字符串转换成B字符串需要的最少操作次数。一个字符串转换为另一个字符串有三种操作：插入(Insertion)、删除(Deletion)、替换(Substitution)。

       A转换成B，对于计算机来讲，比较适合依靠循环逐步把A中的字符转换成与B匹配成功的字符，在这个过程中使用插入、删除或替换操作来实现，比如：A中’k’转换成B中’s’， A中’k’转换成B中’i’，…，A中’i’转换为B中’s’， A中’i’转换为B中’i’，…，类似这样逐个依靠循环实现，显然这与人直接判断哪些位置需要修改是有区别的，若让人修改，直接把首尾改动即可，我们也可以让计算机做这种修改，但这种方式只能解决一种情形，不能推广到其它情形，不适合题目的普遍性的求解问题。既然计算机更适合这种逐步的判断，我们的算法必须也要符合这种计算特点，而且算法应该适合普遍性，这样的算法才有泛化能力。我们需要找到一种普遍的规律，适合计算机对所有字符串之间的转换。

       这种操作是依靠循环来实现的，一般是在循环的索引所到的位置进行插入、删除和替换的操作，而不是随意的位置进行这三个操作。在计算机循环判断中，把一个字符串转换成另一个字符串，就是通过插入、删除或替换来改变前者，最后与后者长度一致，且对应位置的字符相同。下面的分析也实际是基于计算机的这些特点来描述的。

        A[0:i]表示字符串A的前i个字符构成的局部字符串，B[0:j] 表示字符串B的前j个字符构成的局部字符串。在计算过程中i，j是随着循环而取值的，我们可以记dp[i][j]是把A[0:i]转换为B[0:j] 所需的最少操作次数，i，j取到当A[0:i]、B[0:j]分别代表各自整个字符串时，就是最终状态，这也是我们要所求的问题。dp[i][j]可以看作是第ij状态的值。由于下面第ij状态是唯一的，不是多个状态，为了方便表述，把第ij状态也称为dp[i][j]状态，严格来讲，两者应该区分开，特别在有的动态规划中第ij状态有多个子状态时，应该区分开，这样概念更清晰。

      在本例中，插入、删除或替换是实现状态的方式，这三种方式决定了当前状态dp[i][j]是由直接相关的三个状态dp[i][j-1]、dp[i-1][j]、dp[i-1][j-1]参与计算。

       dp[i][j]的计算与直接相关状态有关。在本例中，插入、删除或替换是实现状态的方式，这三种方式决定了当前状态dp[i][j]的直接相关的三个状态为dp[i][j-1]、dp[i-1][j]、dp[i-1][j-1]。插入对应了对dp[i][j-1]状态的操作，删除对应了对dp[i-1][j]状态的操作，替换对应了对dp[i-1][j-1]状态的操作。

       从一个状态到另一个状态都是靠插入、删除或替换中任何一个来实现的。dp[i][j]与直接相关状态有关，它的已产生的直接相关状态有dp[i][j-1]、dp[i-1][j]、dp[i-1][j-1]，而达到某个状态都是靠插入、删除或替换来实现的。

(1)插入操作实现状态转移

        插入操作实现状态转移，dp[i][j]状态只能是由dp[i][j-1]转移过来。由 dp[i][j-1]到dp[i][j]状态，i不变，而j-1到j增加了一个字符，说明状态转移中，A[0:i]的长度不变，而B[0:j]字符窜长度增加了1，因而只能插入操作，才有它们的长度可能一致且出现最佳情况：在A[0:i]末尾插入一个字符就实现了dp[i][j]状态下与B[0:j]转换成功。因此，由dp[i][j-1]状态到dp[i][j]状态最少操作次数是dp[i][j]=dp[i][j-1]+1，其它删除或替换操作都会大于这个次数。

(2)删除操作实现状态转移

         删除操作实现状态转移，dp[i][j]状态只能是由dp[i-1][j]转移过来。由 dp[i-1][j]到dp[i][j]状态， i-1变成了i，而j不变，说明状态转移中，A[1:i]的长度增加了1，而B[0:j]字符窜长度不变，因而只能删除操作，才有它们的长度可能一致且出现最佳情况：删除A[0:i]末尾一个字符就实现了dp[i][j]状态下与B[0:j]转换成功。因此，由dp[i-1][j]状态到dp[i][j]状态最少操作次数是dp[i][j]=dp[i-1][j]+1，其它插入或替换操作都会大于这个次数。

(3)替换操作实现状态转移

      替换操作实现状态转移，dp[i][j]状态只能是由dp[i-1][j-1]转移过来。由 dp[i-1][j-1]到dp[i][j]状态， i-1变成了i，而j-1变成了j，两者都是增加1，说明状态转移中，A[0:i]、B[0:j]的长度在原来基础上都增加了1，因而只能替换操作，它们的长度可能一致且出现最佳情况：替换A[0:i]末尾一个字符就实现了dp[i][j]状态下与B[0:j]转换成功，当A[0:i]中的字符A[i]与B[0:j]中的字符B[j]不相同时，A[i]需要被替换为B[j]，dp[i][j]= dp[i-1][j-1]+1，但当A[i]与B[j]相同时，不需要替换，此时，dp[i][j]= dp[i-1][j-1]，其它插入或删除操作都会大于这个次数。

        dp[i][j]可以由上述三个直接相关状态之一转化而来，因而可以取三个直接相关状态中的最小值min，即为我们所需的最少转换操作次数。上面的描述内容也即是普通情况下的动态规则DP，根据这个DP，我们可以计算出新的状态。

(4)初始值

       下面我们再来确定初始状态。初始状态的源头是空字符转换为非空字符，若A为空字符，B不是空字符，A转换为B[0:j]，用0表示空字符的索引，也即表示初始状态的情形，显然，dp[0][j]=j，相当于不断的插入字符，j为插入字符的个数；若A为非空字符，B为空字符，A[0:i] 转换为B，显然，dp[i][0]=i，相当于不断的删除字符，i为删除字符的个数。当然，我们可以把初始状态从1个字符开始，显然，没有从空字符手动计算方便，初始值一般是手动计算的。

       本例中的初始状态是一种特别情况，需要单独处理，我们可以把初始值和上面的普遍情况统一为下面动态规则DP（状态转移方程）：

简化为：

      上面简化的数学表达式中，①式可以看作是问题的特别情况，单独处理，②式可以看作是问题的普通情况，也即为动态规则DP（也即状态方程）。

       前面我们是从字符串A、B都不为空进行分析，dp[i][j]的索引与字符串的索引是一致的，这种不影响分析，但现在加上刚才增加了空字符这种初始状态，要注意dp[i][j]的索引变成比字符串的索引多一个，如图2-5所示。因此，在代码中注意i、j索引表达的变化，否则，使用不当容易产生异常提示string index out of range。

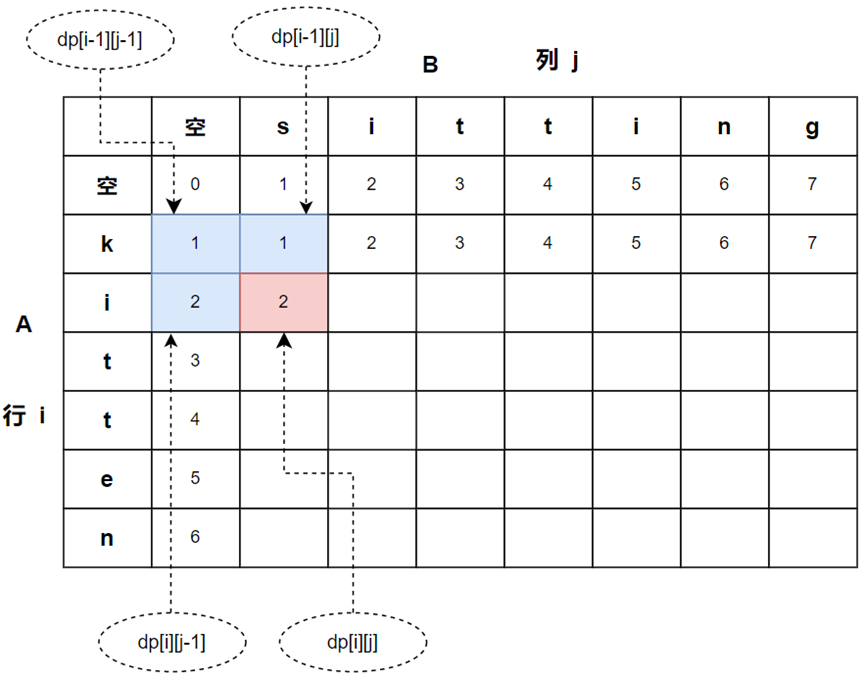
图2-5 编辑距离最少操作次数

        上面的分析及下面代码的实现可以结合下面图2-5来理解。红色区域的状态由周围蓝色的状态决定，即’ki’转换成’s’至少需要操作2次。下面程序代码是实现编辑问题。

1.3动态规划算法代码实现

(1)完整代码

       下面代码是按上述分析过程实现的，完全体现了我们上面对动态规划的论述，从代码中就能看到动态规划算法的思想，我们可以结合下面代码来理解动态规划算法在本问题中的应用。

#编辑距离问题
def edit_distance(A, B):#增加1,因为初始值增加了空字符有关的行列。n, m = len(A) + 1, len(B) + 1#生成一个二层列表,存放状态值。dp= [[0] * m for i in range(n)]#初始值,本例中初始值实际对应为特别情况。#dp[0][0] = 0#定义列表时已赋值。for i in range(1, n):#空字符的处理dp[i][0] = i #也即dp[i][0]=dp[i - 1][0] + 1for j in range(1, m):#空字符的处理dp[0][j] = j#也即dp[0][j]=dp[0][j - 1] + 1#普通情况,这里的i,j索引是dp的索引,0表示空字符,因此,索引从1开始。for i in range(1, n):for j in range(1,m):#下面要注意A、B的索引值,它们的索引不是dp对应的索引值,要减去1,才刚好对应。#因为字符串的索引是从0开始,所以字符串中减去1,当dp到i,j时,由于上面增加了空字符处理的行和列,#所以A[i - 1],B[j - 1]刚好是对应了当前状态dp[i][j]。if A[i - 1] == B[j - 1]:temp = 0else:temp = 1dp[i][j] = min(dp[i-1][j]+ 1,dp[i][j-1]+1,dp[i-1][j-1]+temp)#动态规则(DP)# dp逐行输出for i in range(n):print(dp[i])return dp[- 1][- 1]ed = edit_distance('ki