绍兴做企业网站的公司广东广州重大新闻
写在前面！
1 先验分布和后验分布
三种信息：总体信息、样本信息、先验信息
总体信息：“总体是正态分布”；样本信息：总体抽取的样本提供的信息，是最新鲜的信息；先验信息：在抽样之前就知道的关于统计问题的一些信息【来源于历史资料等】
贝叶斯公式
离散形式：
几个公式：
先验分布：
样本信息的综合：
三个信息的综合：
对进行估计：
求后验分布！！！
【1】连续时（先验分布）
（1）写出先验分布，如果不知道按照均匀分布处理
（2）计算样本X 和参数的联合分布
样本似然函数 乘以 先验信息密度函数
（3）计算X的边际密度【m(x)】
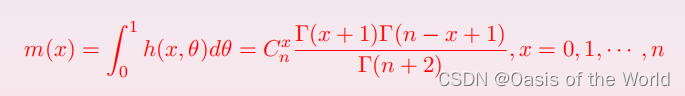
（4）利用贝叶斯公式得到的后验分布
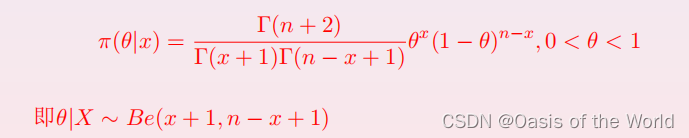
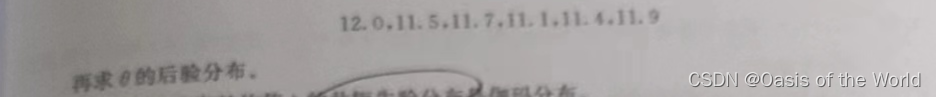
所以的范围在这里就是 大于样本数的的最大值-0.5 小于最小值+0.5
这样就定下了的取值范围咯！！！！
具体视频启发见：已知观测值求后验分布-哔哩哔哩_bilibili
【2】离散
共轭先验分布
【1】正态分布[指的是样本]的共轭先验分布[先验和后验都是]是正态分布(之间的关系)
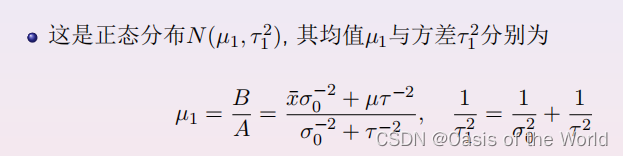
【2】二项分布中的成功概率
的共轭先验分布式贝塔分布
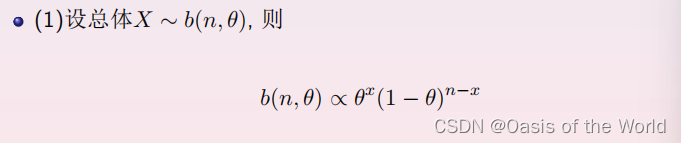
【3】泊松分布的均值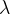
的共轭先验分布是伽马分布
是二项分布的进化，X是发生的次数，那么当抽取样本时，就是总次数！！！！【可见例题5.3.1】
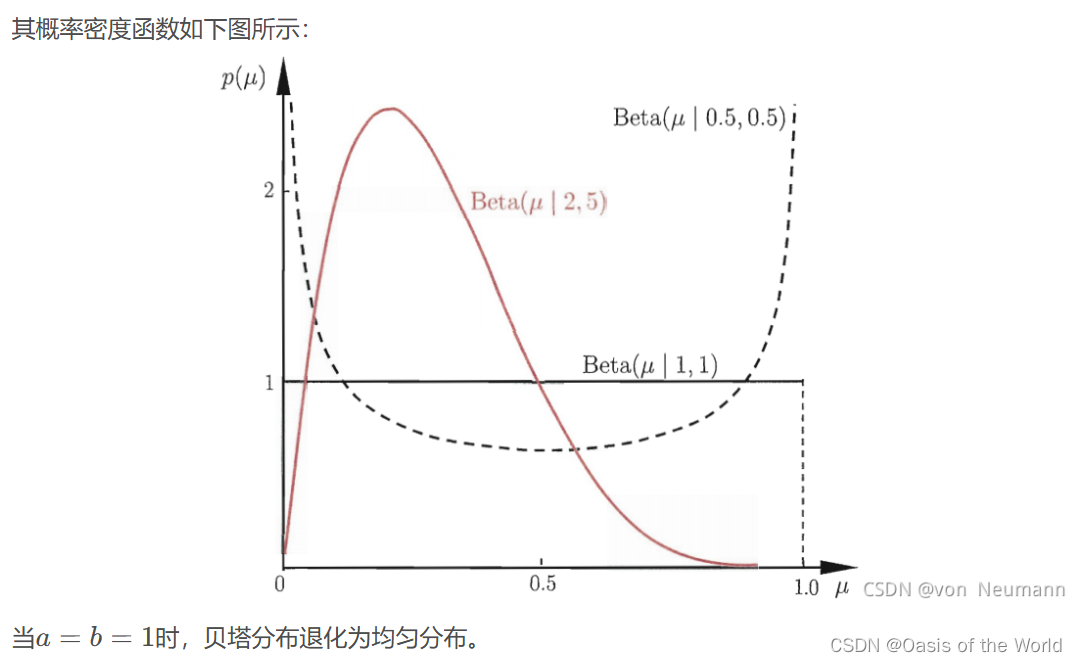
贝塔分布
伽马分布
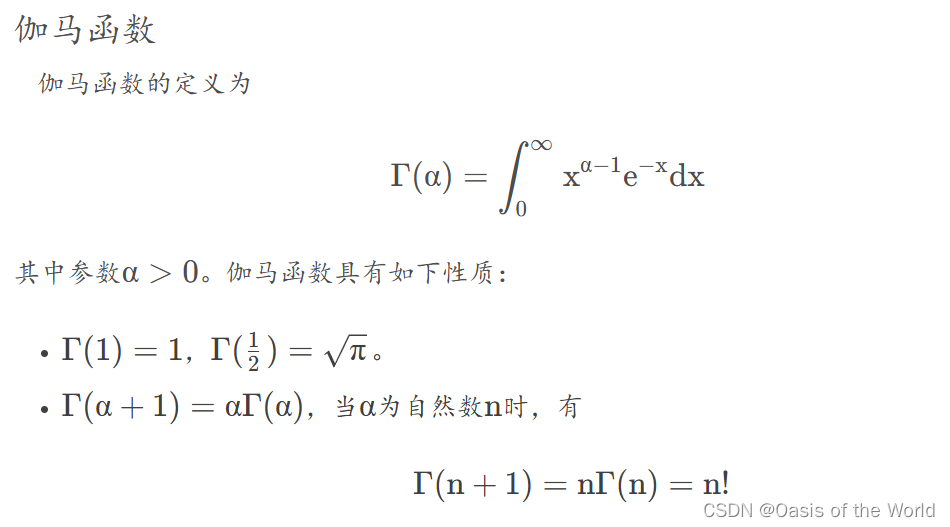
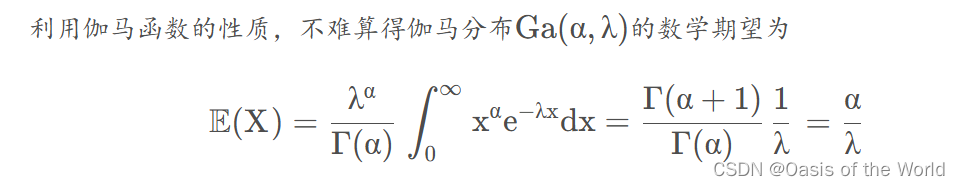
特例：
先验分布超参数的确定
【1】利用先验矩
【2】利用先验分位数
【3】利用先验矩和先验分位数
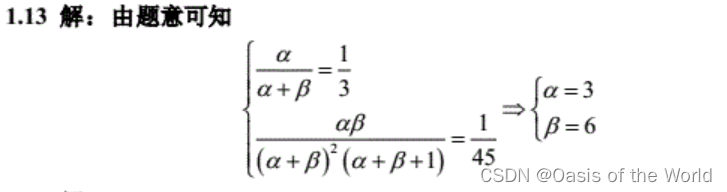
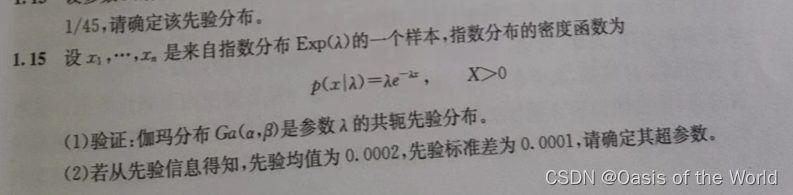
充分统计量【更方便的计算出后验分布！】
作用：
应用：
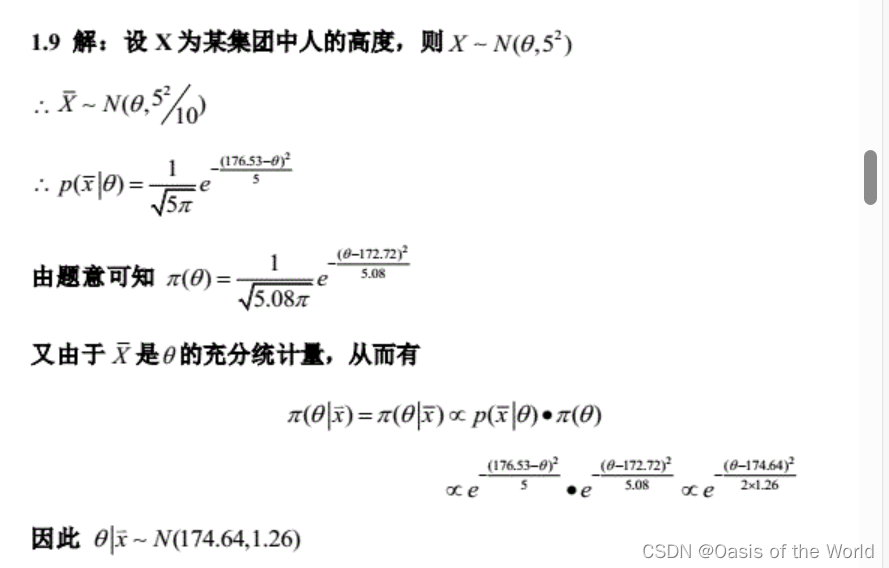
p（x|）是没有办法计算出来的因为，不知道具体取值的情况，但是p（
|
）是知道的
2 贝叶斯推断
存在意义：
2.1 条件方法
2.2 估计
2.2.1 贝叶斯估计
例题1
例题2
例题3
贝叶斯假设 是假设是均匀分布，当都为1 的时候贝塔分布退化成均匀分布
例题4
最大的取值不能超过观察值哦！！！
2.2.2 贝叶斯误差估计
后验均方误差的均值！
例题1 ！！！！（先验分布是离散的）
后验密度达到最大的时候所对应的 是最大后验估计
后验分布期望值是后验分布均值
例题2 （先验分布是连续的贝塔分布）
众数算出来的值其实就是贝塔分布函数达到最大时自变量的取值！！！！
2.3 区间估计
不用寻找枢轴量直接用后验分布就可以！！
例题1
110.38-1.96*8.32 = 94.07
110.38+1.96*8.32 = 126.69
2.4 假设检验
2.4.1 假设检验
接受最大后验概率的假设！！！！
例题1
计算出后验分布！！
均匀
2.4.2 贝叶斯因子
后验概率比较的方法！
后验机会比、前验机会比！可见2.4.4 例题2
贝叶斯因子表示数据X支持原假设的程度！
2.4.3 简单对简单【先计算贝叶斯因子】
例题1
2.4.4 复杂对复杂【计算后验概率比】
例题2
不用计算器的话：就是先标准化然后查表！
贝叶斯因子小这就不可以！
2.4.5 简单对复杂【先计算贝叶斯因子】
例题3
2.4.6 多重假设检验
例题4
谁大接受谁！
2.5 预测
例题5
2.6 似然原理
3 先验分布的确定
3.1 主观概率
3.2 利用先验信息
3.2.1 直方图法（微重要）
例题1
3.2.2 选定先验密度函数形式再估计其超参数
通过矩估计的方法！
例题1延续
例题2
3.2.3 定分位度法和变分位度法【了解即可】
3.3 利用边缘分布确定先验分布
3.3.1 可直接求出边缘分布
例题1
让m(x)达到最大时 ，求出两个超参数的值
3.3.2 混合分布下求出边缘分布类似加权求和
例题2
3.3.3 先验选择的ML-LL方法
例题3 延续3.3.1的例题1
样本是从边缘分布里抽出来的当然可以用于边缘分布超参数的估计！！！！！
3.3.4 先验选择的矩方法
可通过公式进行简化计算！
目标是求出
例题4
到此为止吧，我看不懂.....服了
3.4 无信息先验分布
4 决策中的收益、损失与效用
4.1 决策问题的三要素
4.2 决策准则
4.2.1 行动的容许性
例题1
4.2.2 决策准则【只使用先验信息】
【1】乐观准则（大中选大）
【2】悲观准则（小中选大）
【3】折中准则（加权）
例题
4.3 先验期望准则
例题
例题
这个只计算均值时发现有两个最优行动，因此再计算方差 选择方差小的！！！
P134【课本】
4.3.2 两个性质
都加不变，同一个状态的一行加一样的数不变！
4.4 损失函数
损失函数：“没有转到该赚到的钱！”
4.4.1 从收益到损失
例题【由收益矩阵得到损失矩阵】
损失为，当前位 与赚最多钱时的差距！（状态是一定的！！！）
也是一个状态一算！
例题（已知收益函数的表达式求损失函数！）
对进行积分得到关于a的表达式，然后求出这个表达式的最小值！！！
4.4.2 损失函数下的悲观准则
例题（收益和损失悲观）
注意悲观准则在 收益函数中时（小中选大）；在 损失函数中时（大中选小）
用损失函数进行决策合理一点！
例题
4.4.3 损失函数下的先期望准则
例题
课本【P141】
例题p142
4.5 常用损失函数
4.5.1 常用损失函数
【1】平均损失函数
【2】线性损失函数
【3】0-1损失函数
【4】多元二次损失函数
【5】二行动线性决策问题的损失函数
例题【后序步骤和5.1 中的例题是一样的！】
先求平衡值就是相等的时候的取值！
5 贝叶斯决策
5.1 贝叶斯决策问题定义
先验信息和样本信息 都使用的决策问题！
按照后验平均损失最小 得到贝叶斯决策
优缺点
例题5.1.1P163!!!
让先验期望损失最小是第四章，把弄没，离散的时候是相乘
贝叶斯要在这个机会基础上基础上进行抽样！
5.2 后验风险准则【贝叶斯准则是使用这个的】
5.2.1 后验风险
例题【贝叶斯决策】！！！！！
【1】第四章
【3】贝叶斯
后验分布！：
损失函数的计算后的个数等于：x的取值【抽样后数据的情况】*行动的个数！
损失函数：
行动2：变成只拿出箱子里的两个进行检查 那么需要支付1.6元，然后如果再进行赔偿！
5.2.2 决策函数
5.2.3 后验风险准则
例题5.2.3
例题5.2.4
5.3 常用损失函数下的贝叶斯估计!!!!
5.3.1 平方损失函数下的贝叶斯估计
【1】定理1在平均损失下
【2】定理2在加权平方损失
【3】定理3在多元二次损失函数
例题5.3.1
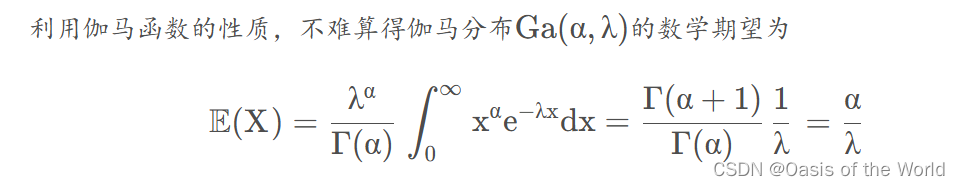
5.3.2 线性损失函数下的贝叶斯估计
【1】定理1
例题5.3.6
后验分布的积分是1
5.3.3 有限个行动问题的假设检验
6 统计决策理论
只使用样本信息！
6.1 风险函数
6.1.1 风险函数
6.1.2 决策函数的最优性
6.1.3 统计决策中的点估计问题
6.1.4 统计决策中的区间估计问题
6.2 容许性
例题
6.3 最小最大准则
例题
例题
