当前位置：首页 > news >正文

口碑营销策略宁德seo公司

news 2025/7/8 10:15:07

口碑营销策略,宁德seo公司,网店怎么开新手,怎么做微信电影网站字典树Trie Tree 字典树也称前缀树，Trie树。在 Elasticsearch 的倒排索引中用的也是 Trie 树。是一种针对字符串进行维护的数据结构。字典树是对词典的一种存储方式，这个词典中的每个“单词”就是从根节点出发一直到某一个目标节点的路径，…

字典树Trie Tree

字典树也称前缀树，Trie树。在 Elasticsearch 的倒排索引中用的也是 Trie 树。是一种针对字符串进行维护的数据结构。

字典树是对词典的一种存储方式，这个词典中的每个“单词”就是从根节点出发一直到某一个目标节点的路径，路径中每个字母连起来就是一个单词。因此它能利用字符串的公共前缀来节省存储空间。

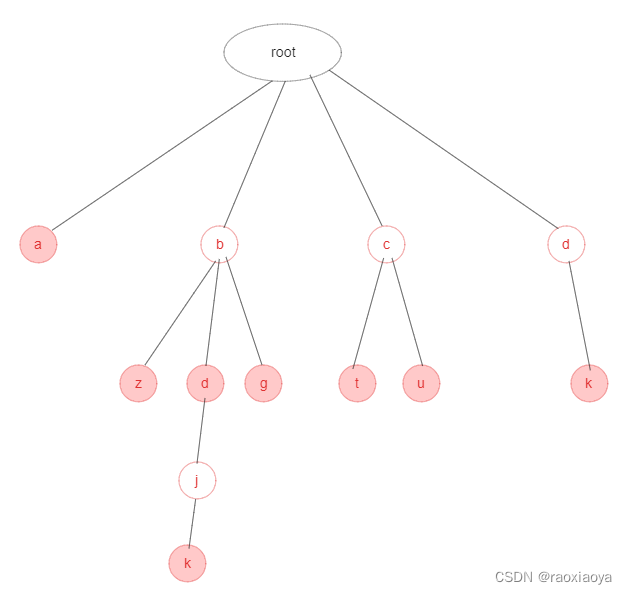
在这里插入图片描述

红色代表有单词在这里结束，因此需要有个标记。上图可以匹配的字符串有：

a
bz
bd
bdjk
bg
ct
cu
dk

具体实现

package mainimport "fmt"type Node struct {nodeId int  // 节点的全局IDexist  bool // 是否有单词在这里结束
}// 255 表示每个节点最多有255个子节点，因为 ASCII 码目前是两个字节，
// 这样做会有一定的空间浪费，但是便于理解，也可以进一步优化。
type Nodes [255]Node// 每个子节点都是数组结构，最终存储到一个map中。
// 层层查找：nodeId -> indexId -> nodeId -> indexId ->...
type Tree struct {nodes         map[int]NodescurrentNodeId int // 自增ID
}func (tree *Tree) insert(str string) {var parentNode Nodefor i := 0; i < len(str); i++ {subIndex := str[i]if _, ok := tree.nodes[parentNode.nodeId]; !ok {var subNode Nodestree.nodes[parentNode.nodeId] = subNode}nds := tree.nodes[parentNode.nodeId]var needUpdate boolif nds[subIndex].nodeId == 0 {tree.currentNodeId++nds[subIndex].nodeId = tree.currentNodeIdneedUpdate = true}if i == len(str)-1 {nds[subIndex].exist = trueneedUpdate = true}if needUpdate == true {tree.nodes[parentNode.nodeId] = nds}// fmt.Println(string(subIndex), nds[subIndex]) // 调试输出parentNode = nds[subIndex]}
}func (tree *Tree) Exist(str string) bool {var parentNode Nodefor i := 0; i < len(str); i++ {subIndex := str[i]if _, ok := tree.nodes[parentNode.nodeId]; !ok {return false}nds := tree.nodes[parentNode.nodeId]if nds[subIndex].nodeId == 0 {return false}parentNode = nds[subIndex]}return parentNode.exist
}func main() {tree := &Tree{nodes: make(map[int]Nodes),}tree.insert("abcdefg")tree.insert("ab")tree.insert("123456789")tree.insert("123456")fmt.Println(tree.Exist("ab"))        // truefmt.Println(tree.Exist("abc"))       // falsefmt.Println(tree.Exist("123456789")) // truefmt.Println(tree.Exist("123456"))    // true
}

压缩字典树 Radix Tree

Radix树，即基数树，也称压缩字典树，是一种提供key-value存储查找的数据结构。radix tree常用于快速查找的场景中，例如：redis中存储slot对应的key信息、内核中使用radix tree管理数据结构、大多数http的router通过radix管理路由。Radix树在Trie Tree（字典树）的原理上优化过来的。

虽然Trie Tree具有比较高的查询效率，但是从上图可以看到，有许多结点只有一个子结点。这种情况是不必要的，不但影响了查询效率（增加了树的高度），主要是浪费了存储空间。完全可以将这些结点合并为一个结点，这就是Radix树的由来。Radix树将只有一个子节点的中间节点将被压缩，使之具有更加合理的内存使用和查询的效率。

在这里插入图片描述