贝尔利网站站长工具一区
六、算法复杂性初步
重要的复杂性类
-
P P P 的定义
-
多项式时间内可解的问题
-
若 L ∈ P L∈P L∈P,则存在确定性多项式时间的图灵机 M M M,使得
M ( x ) = 1 ⟺ x ∈ L M(x)=1⟺x∈L M(x)=1⟺x∈L
-
-
N P NP NP 的定义
-
多项式时间内可验证验证解的正确性
-
(表示非确定性多项式时间而不是非多项式时间)
-
若 L ∈ N P L∈NP L∈NP,则存在确定性多项式时间的图灵机 M M M,使得
x ∈ L ⟺ ∃ w ∈ { 0 , 1 } p l o y ( n ) s . t . M ( x , w ) = 1 x∈L⟺\exist w∈\{0,1\}^{ploy(n)}\ \ s.t.\ M(x,w)=1 x∈L⟺∃w∈{0,1}ploy(n) s.t. M(x,w)=1
注:如果 x ∈ L x∈L x∈L,那么存在一个证书 w w w,使 M M M能够在多项式时间内验证 x ∈ M x∈M x∈M
-
-
N P − h a r d NP-hard NP−hard
- 若一个问题属于 N P − h a r d NP-hard NP−hard,那么它可以在多项式时间内规约成 N P NP NP 问题
-
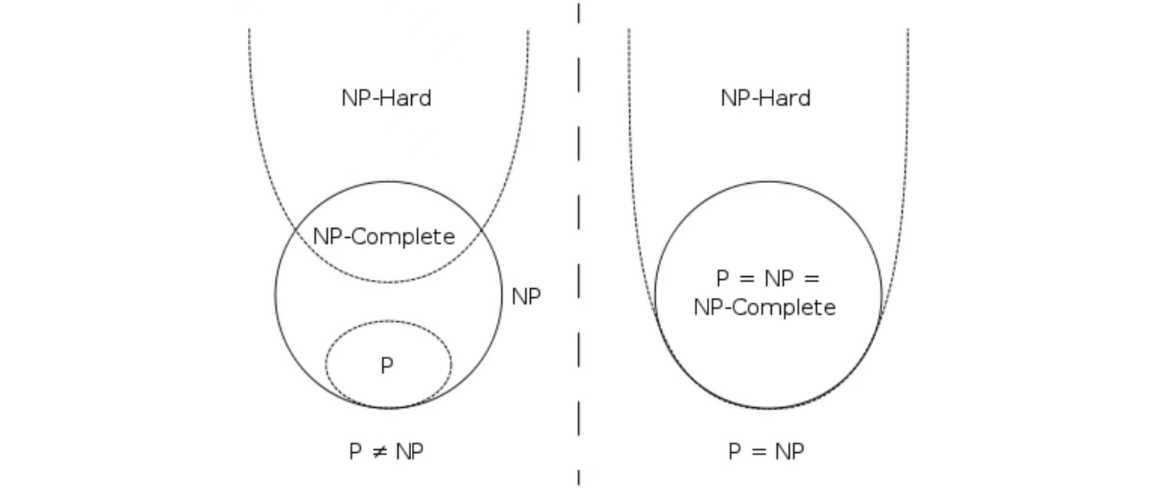
N P − c o m p l e t e NP-complete NP−complete
- 是 N P NP NP和 N P − h a r d NP-hard NP−hard的交集,即 N P C = N P ∩ N P H NPC=NP∩NPH NPC=NP∩NPH
- N P C NPC NPC是 N P NP NP中最难的问题,如果找到多项式时间解决 N P C NPC NPC,那么 P = N P P=NP P=NP
SAT 问题
定义:给定一个布尔逻辑表达式,判断是否存在一个布尔变量赋值,使得整个表达式的值为真。
合取范式(CNF):一种布尔逻辑表达式的标准化形式,若干个句子合取(AND),每个句子中若干个文字析取(OR)
例如,以下一个CNF公式:
( ¬ a 1 ∨ a 2 ) ∧ ( ¬ a 1 ∨ a 3 ∨ a 4 ) ∧ ( a 1 ∨ ¬ a 2 ∨ a 3 ∨ ¬ a 4 ) (\neg a_1 \lor a_2) \land (\neg a_1 \lor a_3 \lor a_4) \land (a_1 \lor \neg a_2 \lor a_3 \lor \neg a_4) (¬a1∨a2)∧(¬a1∨a3∨a4)∧(a1∨¬a2∨a3∨¬a4)
注:存在一种赋值,使其中一个句子为真,整个CNF即为真。
2-SAT问题:每个子句恰好包含2个文字。 P P P 类问题。
3-SAT问题:每个子句恰好包含3个文字。 N P − c o m p l e t e NP-complete NP−complete 问题。
- 例如: ( l 1 ∨ l 2 ∨ l 3 ) ∧ ( l 4 ∨ l 5 ∨ l 6 ) ∧ ⋯ (l_1 \lor l_2 \lor l_3) \land (l_4 \lor l_5 \lor l_6) \land \cdots (l1∨l2∨l3)∧(l4∨l5∨l6)∧⋯
当n>2,n-SAT问题就是NP-hard的。任何n-SAT都可以通过引入新变量的方法转化为3-SAT问题。
随机化算法
ZPP类型
- 保证一定能找到正确答案
- 需要多次运行,可以在期望的多项式时间内找到结果
- 即:保证正确性,运行时间随机性
- 如:随机化快速排序、随机化选择算法
BPP类型
- 不保证得到正确答案,结果可能出错
- 时间是确定的多项式时间
- 即:时间复杂度好,结果不好
- 如:矩阵恒等式测试
6.1 证明: P ⊆ N P P⊆NP P⊆NP
证明:
- 对于 P P P问题的图灵机 M M M,构造另一个图灵机 M ′ M' M′:输入是 w w w和 x x x,对于相同的 x x x有相同的输出, w w w对输出无影响
- 当 x ∈ L x∈L x∈L时, M ( x ) = 1 M(x)=1 M(x)=1,存在 w ′ ∈ 0 , 1 p l o y ( n ) w'∈{0,1}^{ploy(n)} w′∈0,1ploy(n), M ′ ( x , w ′ ) = 1 M'(x,w')=1 M′(x,w′)=1
- 当 x ∉ L x ∉L x∈/L时, M ( x ) = 0 M(x)=0 M(x)=0,对于任意的 w w w, M ′ ( x , w ) = 0 M'(x,w)=0 M′(x,w)=0
- 显然 M ′ M' M′是确定性多项式图灵机,结合 N P NP NP问题定义,存在 w ′ ∈ 0 , 1 p l o y ( n ) w'∈{0,1}^{ploy(n)} w′∈0,1ploy(n), M ′ ( x , w ′ ) = 1 M'(x,w')=1 M′(x,w′)=1,验证解是否正确。所以该 P P P问题也是一个 N P NP NP问题,所以 P ⊆ N P P⊆NP P⊆NP。
6.2 证明: 如果存在 N P NP NP 难的问题 Π ∈ P Π ∈ P Π∈P,则 P = N P P = NP P=NP
证明:
- 根据 Π ∈ P Π ∈ P Π∈P,得 Π Π Π在多项式时间可解决
- 根据 N P − h a r d NP-hard NP−hard 定义,所有 N P NP NP问题 F F F可在多项式时间内规约到 Π Π Π,即 F ∈ N P F∈NP F∈NP,有 F ≤ p Π F≤_pΠ F≤pΠ
- 所以 F F F在多项式时间转化为 Π Π Π,再多项式求解 Π Π Π,整个过程是多项式时间完成的,所以 N P ⊆ P NP⊆P NP⊆P
- 又已知 P ⊆ N P P⊆NP P⊆NP,所以证得 P = N P P=NP P=NP。
6.3 证明:如果 N P = P NP=P NP=P,则单向陷门不存在。
- 假设算法
Invert用来寻找函数 f f f的逆映射:利用一系列语言 L i Li Li,表示是否存在 w w w使得 y = f ( z ∣ ∣ w ) y=f(z||w) y=f(z∣∣w) - 根据文本内容, L i Li Li属于 N P NP NP,同依据条件,也属于 P P P
- 如果 P = N P P=NP P=NP,那么该算法能在多项式内求解,即找到了函数 f f f的逆映射,也就是找到 x x x使得 f ( x ) = y f(x)=y f(x)=y
- 综上,若 N = N P N=NP N=NP,多项式时间可破坏单项函数的不可逆的性质,则单向陷门不存在
